Algoritmos tradicionales de la multiplicación y de la división con billetes.
Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.
Algoritmos tradicionales de la multiplicación y de la división con billetes.

Para los nuevos. Con esto de los algoritmos (con los tradicionales y con cualquiera) hay que tener claro que el papel principal que deben jugar en el aprendizaje no es el mismo que el que pudieran tener hasta mediados del s. XX. No tienen la misma importancia social que entonces.
Habrá que poner el foco en el desarrollo del sentido numérico, la estimación y técnicas de cálculo oral y mental. Así mismo, trataremos de profundizar en la comprensión de nuestro sistema de numeración posicional.
Una propuesta adecuada, por ejemplo, evitaría el uso de algoritmos en 1º EP, porque en el momento que los introduces y pones ahí el centro de atención, olvídate del cálculo mental. Tiene sentido introducirlos hacia finales de 2º EP, con números de tres cifras.
Pero entonces… ¿cómo los pongo a hacer problemas si no saben ni sumar? Bueno, pues es que una cosa es sumar y resolver situaciones aditivas y otra es cómo llegues al resultado de la suma.
De hecho, centrarte en los algoritmos hace que dediques muy poco tiempo a otras cosas. Confunden idea de suma con procedimiento para sumar. Y entonces los problemas son o de suma o resta. Y me lo juego, si es la una será la otra. Datos, operación, solución. Hombre llevándose la palma de la mano a la cara
Algoritmo de la multiplicación
Venga, al lío. Vamos a justificar con billetes el algoritmo tradicional de la multiplicación por un número de una cifra. Representamos el número 1426 con el menor número de billetes posible.

Esto ya es una situación interesante. Con el MENOR NÚMERO DE BILLETES. Si hubiese usado 26 billetes de uno, podría haber cambiado 20 de ellos por 2 billetes de diez.
Construye ahora una cantidad de dinero tres veces mayor. De nuevo, represéntala con el menor número de billetes posible. Pasaré a tener 18 billetes de uno, 6 billetes de diez, 12 de cien y 3 de mil.

Pero como tengo 18 billetes de uno, puedo cambiar 10 de esos por 1 billete de diez. Y como tengo 12 billetes de de cien, puedo cambiar 10 de esos por 1 billete de mil. Esos cambios van a ser las llevadas.
Pd. Para este hilo he tenido ayuda.

Veamos ahora el algoritmo en relación con las acciones que hemos hecho con los billetitos. El primer paso es escribir el número grande arriba (multiplicando) y el pequeño debajo (multiplicador). Bien alineados

Triplicamos los billetes de uno. Nos salen 18.

Pero 10 de esos los podemos cambiar por 1 de diez. De ahí viene el “y nos llevamos una”.
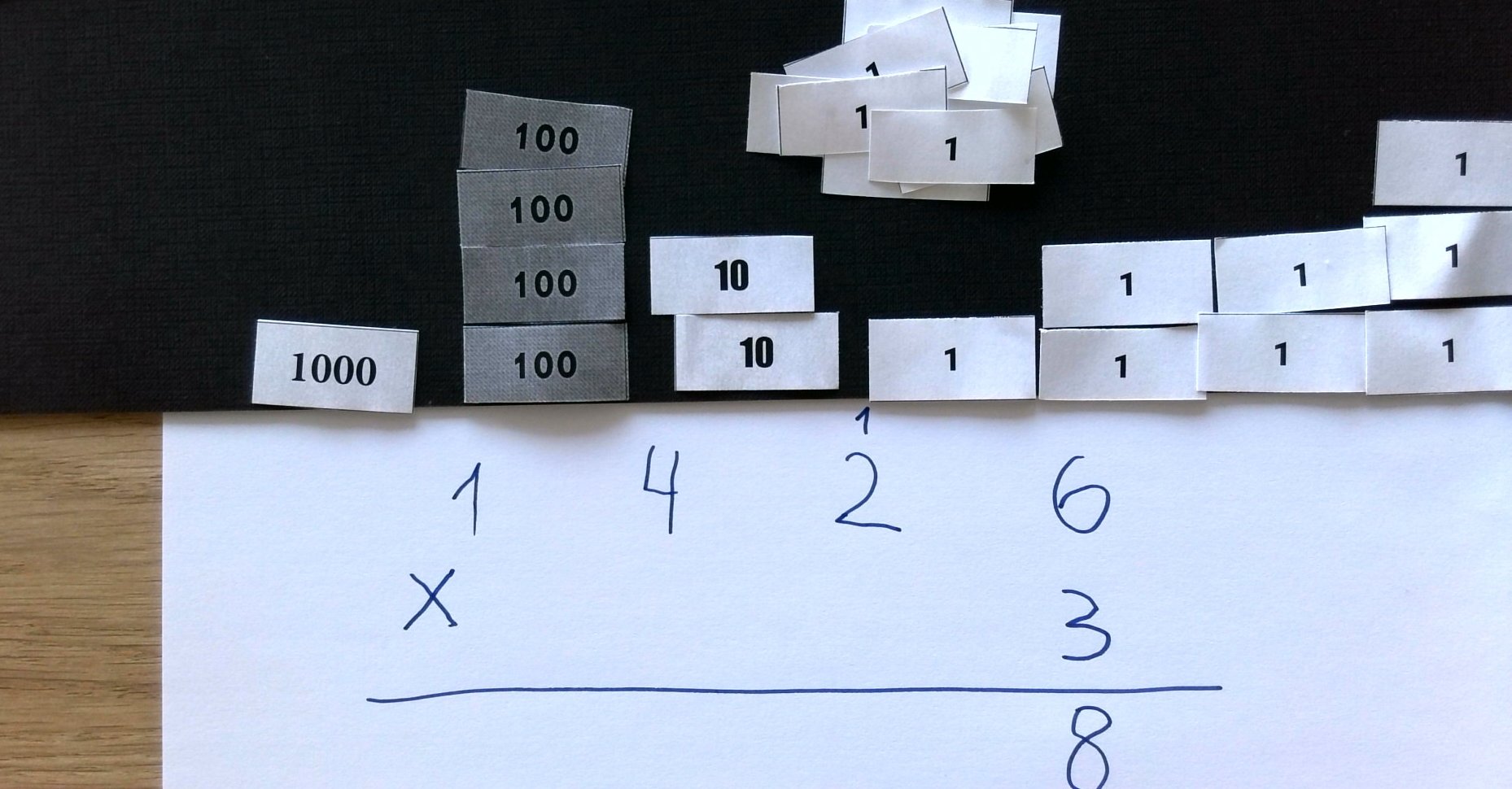
Se pasa a multiplicar la siguiente cifra del multiplicando, a cuyo resultado añadiremos la “llevada” que hemos guardado del paso anterior.
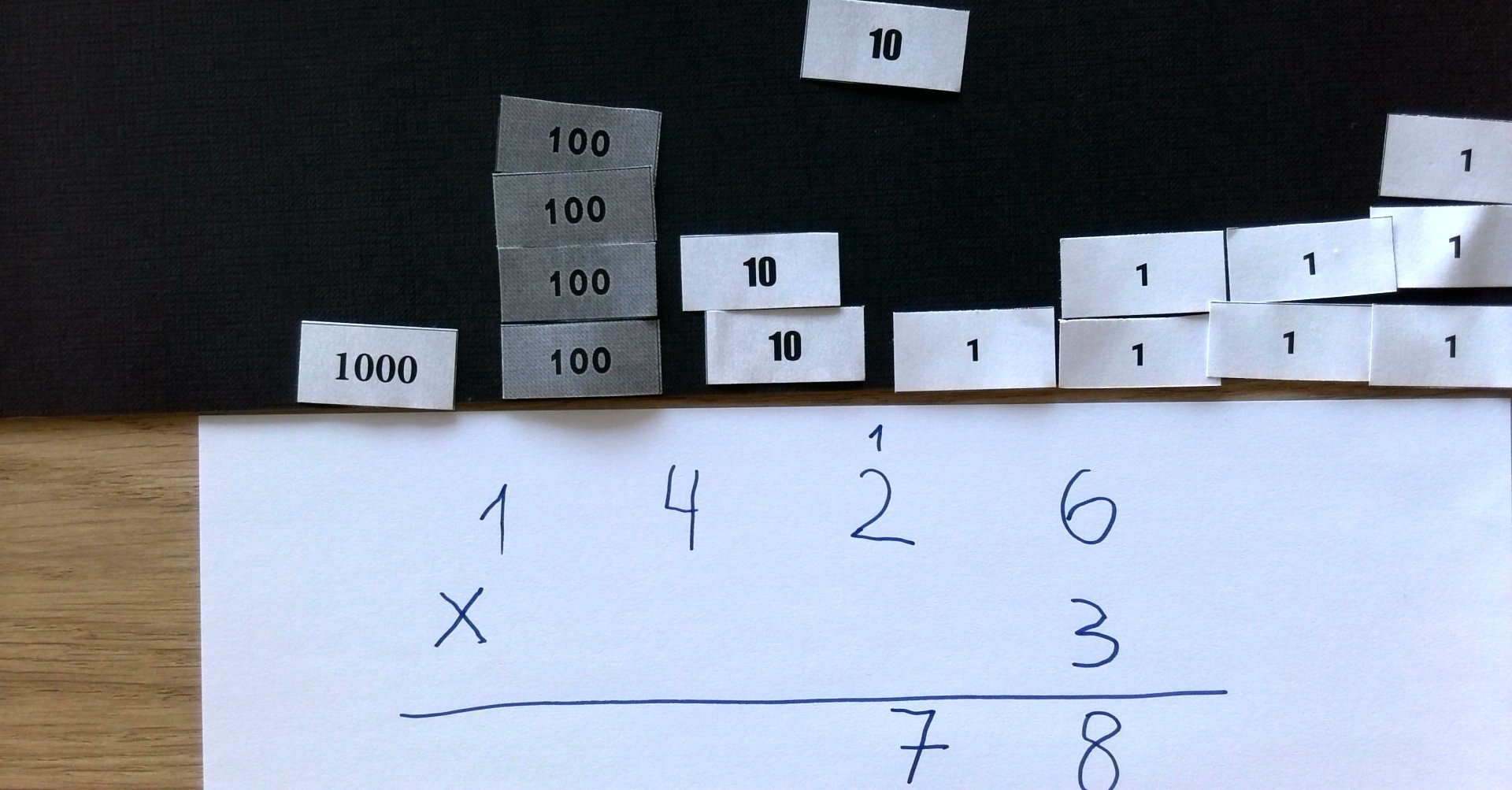
Se procede de la misma manera hasta llegar a la última cifra del multiplicando. El resultado de esta última se escribe íntegro.

Vamos a por la multiplicación por un número de dos cifras. Como paso previo, veamos qué ocurre cuando multiplicamos un número por 10.
La tarea es igual que la anterior. Representa el número 327 con la menor cantidad de billetes posible. Entonces, construye una cantidad 10 veces mayor y represéntala con el menor número de billetes posible.
Lo que ocurre es que, en este caso, te juntas con 70 billetes de uno, 20 de diez y 30 de cien; que puedes cambiar por 7 de diez, 2 de cien y 3 de mil. En definitiva, tienes ante ti el número 3270.
Por eso cuando multiplicamos por 10 basta con añadir un cero a la derecha. Nos apoyamos, como se ha visto, en que diez unidades de un orden equivalen a una unidad de un orden superior.
Ahora sí estamos en condiciones de multiplicar el 327 por un número de dos cifras, como el 24. Habiendo trabajado técnicas orales de cálculo, discutimos en clase que para hacer una cantidad 20 veces mayor, podemos duplicarla primero y luego construir algo 10 veces mayor.
Después de haber manipulado con algunos ejemplos, reflexionamos y justificamos el algoritmo, relacionando los pasos de este con las acciones realizadas.

Realmente, como veremos, hacer una cantidad 24 veces mayor que otra, es lo mismo que hacer una cantidad 4 veces mayor, una cantidad 20 veces mayor, y sumar ambos resultados.
Si quiero hacer mentalmente 35x24, puedo pensar en hacer 35x20, que se puede hacer duplicando 35 y multiplicando por 10 (sale 700). Luego le sumo lo que falta, 35x4, que es 140, número al que puedo llegar duplicando 35 y volviendo a duplicar el resultado. Total, 700+140=840.
Que me voy por las ramas. Estábamos en 327x24. Primero, multiplicamos por 4 el multiplicando, cosa que ya sabemos hacer. Ahí tenemos el 1308.

Si recordáis el algoritmo, ahora pasamos a multiplicar 327x2, pero el resultado lo ponemos desplazado. Esto es porque estamos duplicando y multiplicando por 10, que ya sabemos que es añadir un cero (por lo que hemos explicado antes). Ese 654 es en realidad un 6540.

Y ahí tenemos el resultado final, al sumar ambas filas.

El “problema” está en que no se suele justificar ese desplazamiento de la segunda fila, con lo cual tenemos a gran parte del alumnado ejecutando un algoritmo sin saber lo que está haciendo para algo que en realidad no le hace falta.

Algoritmo de la división
Lo de la división, que parece que trae más de cabeza al personal, ya lo traté de pasada en el de las tortillas, hilo que enlazaré después. La cuestión es que voy a presentarlo aquí como el reparto de una cantidad de dinero.
Comenzamos igual que antes. Representa el número 6284 con el menor número de billetes posible y reparte esa cantidad entre 6 personas. Cuando esto se plantea así, sin más, tampoco hay por qué ir en orden, pero van a salir elementos clave en los que se apoya el algoritmo.

Por ejemplo, un niño o una niña podrían empezar repartiendo los billetes de diez. Como hay 8, pueden dar 1 billete de diez a cada participante. Sobran 2. También pueden dar 1 billete de mil a cada uno, y en este caso no sobra ninguno.
Me quedan por repartir entonces 2 billetes de cien, 2 de diez y 4 de uno (es decir, 224). Está claro que puedo seguir repartiendo. Vaaaale, cambio los 2 de cien por 20 de diez y sigo repartiendo, porque ahora puedo dar 3 de diez a cada uno y me sobran 2 de diez.
Y así puedo seguir hasta ver que a cada participante le tocan 1047 y que sobran 2 billetes de uno. Nota: he elegido un ejemplo en el que sale un cero en el cociente que suele ser fuente de dificultades. Se puede empezar con otros que no incluyan estos ceros.
Sin embargo, quiero ilustrar que teniendo un control semántico sobre lo que estamos repartiendo en cada momento, evitamos que se «olvide» ese cero y que el resultado final no tiene sentido. Cosa que, con algo de sentido numérico, se vería al instante (¡¡no puede ser 147!!)
Cómo justificamos el algoritmo. El tradicional en España tiene la siguiente pinta inicial.
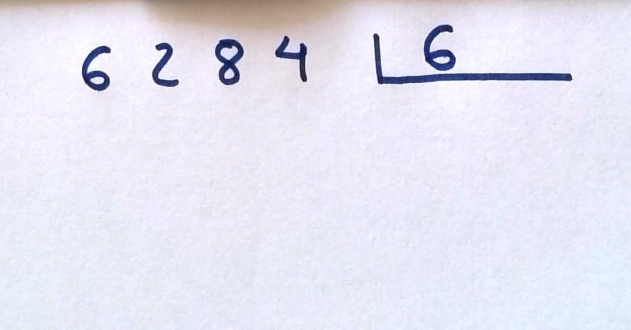
Lo voy a describir desplegado del todo, para incidir en todo lo que está pasando. Esto suele llamar la atención, porque si se usa el algoritmo tradicional de la resta (el que modifica el sustraendo), no suele escribirse lo que se resta, sino que se hace “on the fly”.
Hay alumnos que cuando hacen lo de la división, no saben que están restando. Y no es culpa suya.
Tenemos esto. Empezamos por la cifra de mayor valor posicional. ¿Cuántos billetes de mil puedo dar a cada uno de los 6 participantes? A ver, tengo 6, pues puedo dar 1 billete de mil a cada uno.

Aquí lo tenemos. He dado 1 billete de mil a cada uno y por eso esto irá en la cifra del cociente correspondiente a las unidades de millar. He dado 6 billetes de mil en total y no me sobra ninguno.

Vamos ahora con los billetes de cien. Tengo solo 2 de cien, por lo que los participantes no van a recibir ningún billete de cien.

Si quiero continuar, con el algoritmo habitual se dice que “bajamos el 8”. Lo que hacemos en realidad es convertir los 2 billetes de cien en 20 billetes de diez, que junto con los 8 de diez del dividendo, nos hacen un total de 28 billetes de diez a repartir entre 6 personas.

De esos 28 billetes de diez, puedo dar 4 a cada uno de los 6 participantes, dando en total 24. Me sobran 4 billetes de diez.

Igual que antes, cambio esos 4 billetes de diez por 40 de uno, que añadidos a los 4 “que bajan del dividendo” me hacen un total de 44 unidades.

Y ya estaría. De esas 44 unidades, puedo dar 7 a cada uno de los participantes, doy un total de 42 y me sobran dos unidades.

La idea de reparto permitirá conectar más adelante representación decimal y fraccionaria del número racional. Más información sobre esto aquí en el de las tortillas, donde ya hablaba de esto de la división.
¿Y cuando el divisor es un números de dos cifras? Bueno, ya sabéis que hay países que no lo tienen en el currículo. No tiene mucho sentido perder mucho tiempo en ello. Pero vaya, se justifica igual que la que acabamos de hacer. Lo que ocurre es que es tedioso.
Fijaos si son tediosas las divisiones estas que he puesto un número donde no era en una de ellas y he usado tippex para no repetir el asuntoHombre llevándose la palma de la mano a la cara. Espero que me perdonéis. Yo nunca lo haría, porque soy de elogiar el tachón Rodando por el suelo de risa.
Y con esto ya estaría. En el hilo de los algoritmos de la suma y de la resta (tradicional y anglosajón) dejé unas plantillas muy cutres para los billetes. Recuerdo que vale con material estructurado de base decimal (puntos, barras y placas, casi mejor).
Todo esto está basado en las prácticas preparadas por @dm_unizar en @FacultadEducaUZ para Didáctica de la Aritmética I.
¡Un saludo y feliz clase! Si has encontrado interesante el hilo, ya sabes, a compartir.
Epílogo
El siguiente hilo, sobre el tratamiento de la medida en diferentes etapas.
Pd. Me dicen por el pinganillo que son muy pequeños estos billetines. Sí, lo son, son los que imprimí en casa para trabajarlo con mis pequeños. Mejor más grandes y, como he dicho en el hilo, mejor puntos, barras y placas, por lo menos para los de la suma y resta.
Aunque no me diréis que no habéis pensado en un kit individual para tiempos pandémicos. En cualquier caso, tened en cuenta que esto se supone que se plantea para niños y niñas de 2ºEP (hacia mitad de curso) y 3ºEP. Antes, como he dicho, ni hace falta ni viene bien.

Pd2. Siempre que hago un hilo sobre esto me gusta mencionar que las matemáticas en primaria no son sólo aritmética. Al igual que las mates en secundaria, que no son solo álgebra.