Sumas y restas con llevadas. Traditional flavour. Usando billetes.

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

Sumas y restas con llevadas. Traditional flavour. Usando billetes.

Ahora que tengo vuestra atención, debo deciros que el tuit anterior lo tiene todo mal. En primer lugar, no hay «sumas con llevadas». En todo caso, se puede hablar del algoritmo tradicional o estándar con llevadas. Digo esto porque 23+18 es una suma. Punto.

Puedo calcular 23+18 sumando 20 a 23 (en lugar de sumar 18) y quitando 2. Total, 41. O puedo hacer 23+10, que da 33, y luego sumar 8, cosa que hasta podría hacer contando con ayuda de los dedos.

O sea, que una cosa es sumar, restar, multiplicar y dividir, y otra, la forma de hacerlo. Los algoritmos tradicionales son UNA FORMA de efectuarlas. Más turra sobre implicaciones educativas de esto al final del hilo.

En el gif salen billetes porque voy a justificar los algoritmos con billetes, pero esos del Monopoly no sirven. No hay de 1 €, ni de 10 €, y además hay de 2000 €, 5000 € y 50000 €. Necesitamos un sistema de billetes estrictamente decimal, desde la unidad.

Como estos de aquí. Tranquilidad, que al final dejaré plantillas. Sosillas como estas (pero que son pequeñas e incluso pueden proponerse kits individuales para el contexto actual) y otras más realistas.

De todas maneras, dependiendo de la edad, sería mejor utilizar material del tipo de puntos, barras y placas. Se diferencia de los billetes en que la barra se ve que está compuesta por 10 puntos.

Dicho todo esto, vamos al lío. La suma. Comenzamos representando los dos números que queremos sumar, con el menor número de billetes posible. Pongamos como ejemplo que quiero hacer 356+878.

Ya con la representación de los números tenemos un interesante problema. Con el MENOR número de billetes posible. Es decir, que esto de aquí no nos vale, aunque represente el 356.

No nos vale porque podemos cambiar 10 billetes de uno por 1 billete de diez.

Aquí tenemos el 356 y el 878.

Ahora juntamos las del mismo tipo y contamos. Me salen 14 billetes de uno. ¡Pero puedo cambiar! Recordemos que quiero utilizar el menor número de billetes posible, así que si puedo cambiar 10 de uno por 1 de diez, lo hago.

Y si hago esto con las demás, ocurre lo siguiente:

¿Qué ocurre en el algoritmo tradicional o estándar de la suma?

Pues que cuando hago 8+6 y me sale 14, digo que pongo 4 y «me llevo una». Ese «me llevo una» es la decena del catorce. En lo que hemos hecho antes, viene de que podemos cambiar 10 billetes de uno por uno de diez.

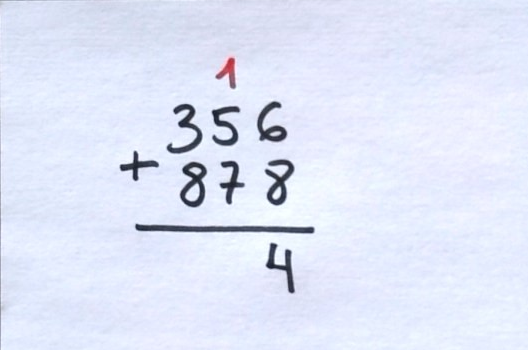
Es tan icónico esto del «y me llevo una» que es el título de un libro de @tocamates 😉. Aquí es fácil de comprender qué es eso de la llevada, pero luego veremos que en el de la resta tradicional no lo es tanto.

Se llaman algoritmos porque son una serie de instrucciones sistemáticas. O sea, que se pueden programar. Este es el de la suma:

1. Escribe los sumandos uno debajo de otro de manera que las unidades de un mismo orden de los diferentes números queden situadas en la misma columna.
2. Traza una raya horizontal debajo del último sumando.
3. Suma las cifras que se encuentran en la columna de la derecha.
4. Si el resultado de la suma es menor que 10, escríbelo en dicha columna debajo de la raya y pasa a sumar la columna siguiente. Si no, salta al paso 5.
5. Si el resultado de la suma es mayor o igual que 10, escribe sus unidades en la columna actual y añade la cifra de las decenas a la suma de la columna siguiente.
6. Continúa el procedimiento (vuelve a paso 3) hasta llegar a la última columna.
7. El resultado de sumar la última columna se escribe íntegro debajo de la raya.
8. El número que aparece debajo de la raya es la suma de dichos sumandos.

Aquí está la suma anterior completa. Los unos en rojo son «las llevadas»; es decir, los cambios que hemos hecho. Observemos que la última suma («el doce», doce centenas) se pone íntegra (una unidad de millar y dos centenas), tal y como indica el algoritmo.

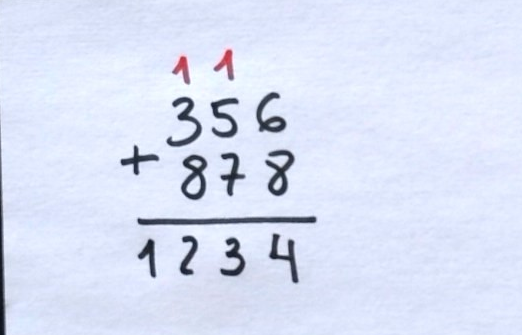
Inciso: una actividad muy maja sería programar estas cosas en Scratch.

Algoritmos de la resta: tradicional (en España) y anglosajón

Vamos con la resta. Explicaré dos algoritmos. El anglosajón y el tradicional (el estándar, en España). El anglosajón es más fácil de justificar y, por tanto, de comprender. Luego tiene alguna implicación que hay que tener en cuenta, pero sin mayor importancia.

Hagamos 425-178. Represento 425 con el menor número de billetes posible. Restar 178 significa quitar (sustraer) 8 billetes de uno, 7 de diez y 1 de cien. Pero, ¿qué ocurre? Que no puedo quitar 8 de donde solo hay 5. Solución anglosajona, cambiar uno de los billetes de 10.

Aquí el algoritmo anglosajón completo con billetes y en notación simbólico-numérica.

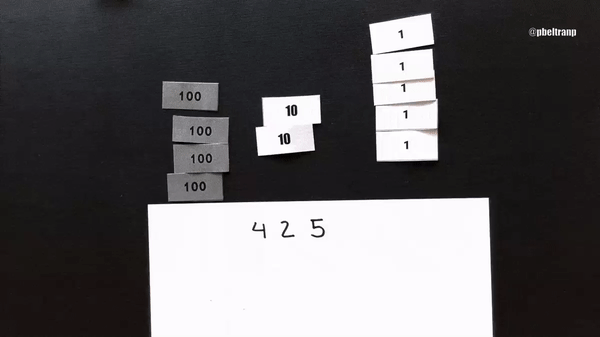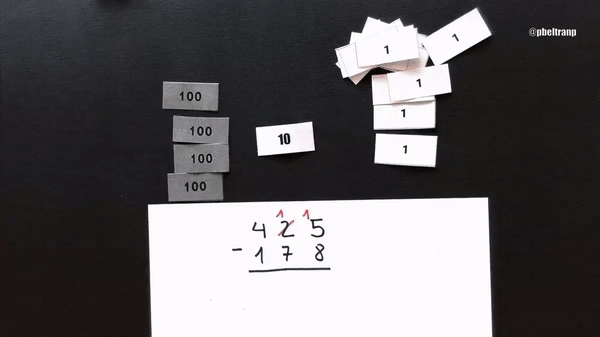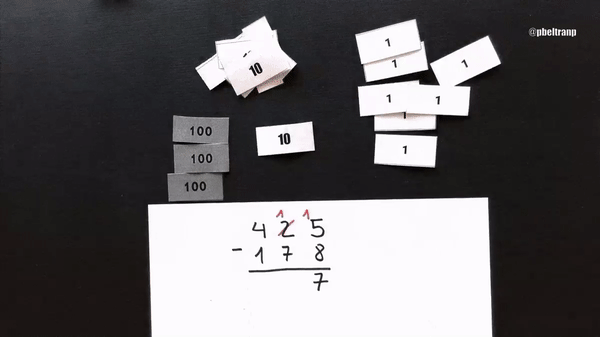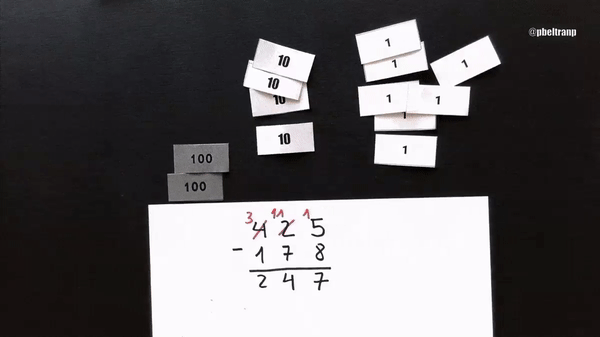
Una característica fundamental del anglosajón es que, para poder hacer la resta, solo se modifica el minuendo (el de arriba). El sustraendo permanece igual.

El anglosajón se basa en que 425 = 410 + 15. Es decir, que puedo cambiar 1 unidades de un orden por 10 unidades del orden inferior. Por ejemplo, 1 decena por 10 unidades; o 1 centena por 10 decenas. Según me convenga.

El tradicional o estándar (en España) se basa en una compensanción. Antes de introducirlo hay que tener claro que si tú tienes 25 euros y yo 10, tú tienes 15 euros más que yo. Y que si nos dan 10 euros a ti y otros 10 euros a mi, seguirás teniendo 15 euros más que yo.

Parece una tontada, pero no es evidente. Sobre todo cuando hablamos de niños y niñas de 7-8 años y que «la llevada» del tradicional tiene que ver con esto. Hay muchísimos alumnos que no llegan a entender qué es la llevada. Lo hacen, y punto.

Vamos a verlo con billetes. 425-178, como antes. Representamos 425 con el menor número de billetes posible. Restar 178 implica quitar 8 billetes de uno, 7 de diez y 1 de cien. Pero no podemos quitar 8 de uno. Así que cojo 10 billetes de uno del montón y los añado a los cinco.

Pero claro, para compensar tengo que añadir la misma cantidad al sustraendo. Añado 1 billete de diez. Esa es la llevada del tradicional. Aquí lo represento (y en simbólico-numérico he escrito más de lo que normalmente se escribe).

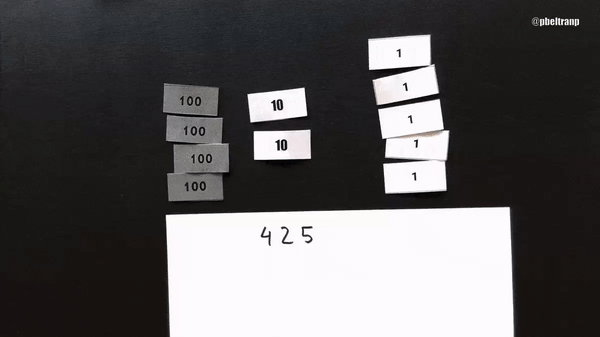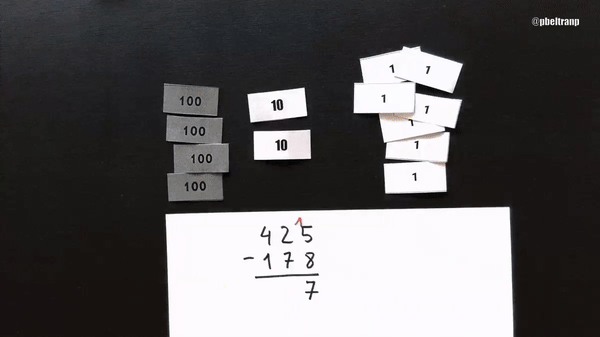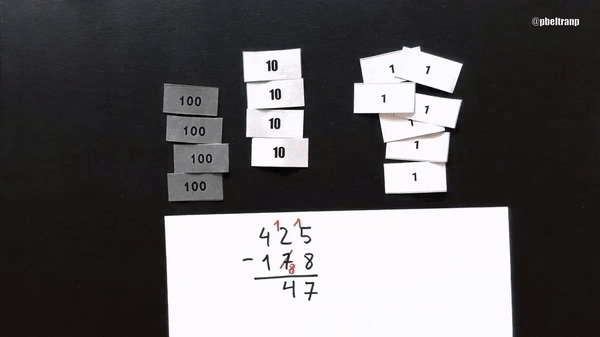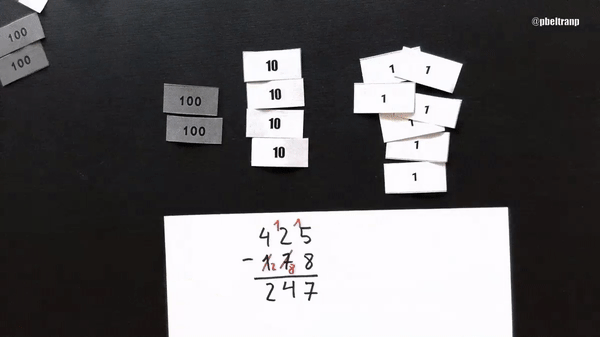
La compensación en que se basa el algoritmo tradicional es la siguiente:

$$425-178 = (425 +10 ) - (178 +10)$$

Volvamos al anglosajón. Una vez aprendido como antes, hay que poner sobre la mesa qué ocurre cuando tenemos ceros intermedios en el minuendo. Tal y como lo hemos hecho, no sirve. Os planteo como ejercicio hacer 2001-975. ¿Qué instrucciones adicionales necesita el algoritmo?

Y el tradicional, ¿tiene este problemilla? Intentad hacer el 2001-975.

No tiene el problemilla del anglosajón. Sin embargo, cuando el sustraendo tiene menos cifras que el minuendo, hay lugares vacíos en las cifras de órdenes superiores. En esos casos, hay niños que no compensan la llevada porque son lugares vacíos.

A los que os enseñaron el tradicional, sabed que seguramente también hayáis restado alguna vez con el anglosajón. Y si no, pensad en cómo hacéis para calcular intervalos temporales expresados en horas, minutos y segundos.

El anglosajón implica, más adelante, que en la división se tienen que escribir las restas parciales. Se necesitan, porque se va escribiendo sobre el minuendo. El tradicional, en cambio, se hace on the fly y no suelen ponerse.

Para terminar, la turra prometida. No se debería enseñar ningún algoritmo (ni estos ni otros) en 1º de Primaria. Y en 2º, únicamente que se manejen los alumnos mentalmente y con diversas estrategias con números de dos cifras. Vamos, que con números de 3 cifras.

Si introducimos algoritmos de forma prematura vamos a anular esas estrategias de cálculo mental. Que, por cierto, pueden aparecer de forma espontánea, pero hay que trabajarlas y discutirlas en clase.

No solo eso, sino que muchos alumnos asimilarán suma y resta con sus algoritmos.

El objetivo de introducir estos algoritmos será el de comprender cómo funciona el sistema decimal posicional. Son adecuados, ya que explotan al máximo sus características. El objetivo, desde luego, no es que hagan N operaciones en 30 minutos.

Más objetivos de aprendizaje: valorar si me compensa hacer la operación de una forma o de otra, estimar lo que va a salir antes de hacerla.

Las plantillas: aquí. Recordad que sería mejor con puntos, barras y placas. Y dejar esto, quizá, para la multiplicación y la división.

Esto que os he contado está basado en una de las prácticas de Didáctica de la aritmética I que se hacen en Zaragoza desde hace mucho, antes de que yo llegara. Así que crédito para @dm_unizar en la Facultad de Educación de la Universidad de Zaragoza.

Si os portáis bien, el año que viene continúo con la multiplicación y la división.

Pd1. Todo esto en paralelo con situaciones concretas (problemas). Y recordando dos cosas:

• Que la aritmética no solo es hacer cuentas.
• Que las matemáticas en primaria no son solo aritmética.

Pd2. Aquí un pequeño test.

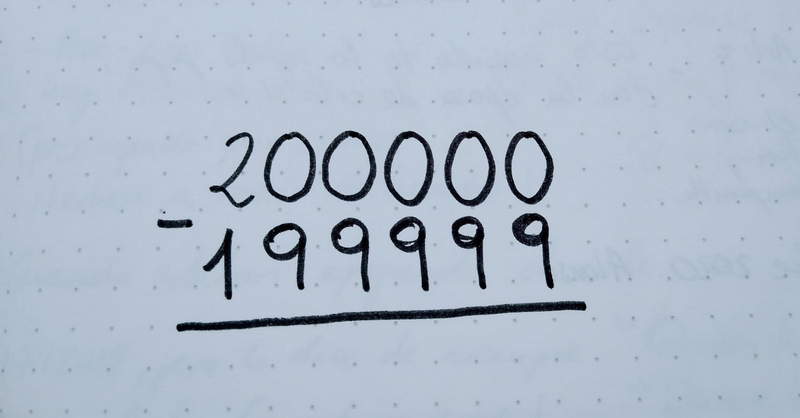
Pd3. Hubo un tiempo en que hacía falta dominar estas técnicas de cálculo para el día a día. De ahí a verlas hoy en día sin comprensión (que, como muestra el hilo, se puede), hay un trecho. Mirad aquí cómo se apañaban hace no tantos años.