Comparación y orden de fracciones, unpacked

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

Comparación y orden de fracciones. Unpacked.

Esto comenzaba con una pregunta.

¿Qué te sugiere esto de aquí?

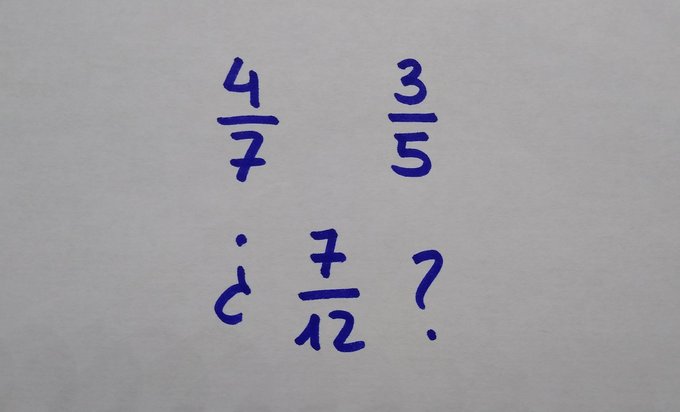
A la cosita de arriba se le puede dar sentido desde el significado de reparto. Pero si recordáis, ayer vimos la multiplicación de fracciones desde el significado, o modelo, de medida. Ambos están relacionados, y no es que tengamos que decantarnos por uno o por otro.

En el de medida, lo de arriba (numerador) es el número de subunidades que necesitamos para medir una cantidad de magnitud. Lo de abajo (denominador), indica las partes iguales en que hemos dividido la unidad para hacer mi subunidad.

En el de reparto, el numerador son los objetos a repartir, mientras que el denominador son los participantes en el reparto, el cual ha de ser equitativo. Es decir, todos los participantes reciben la misma cantidad.

¿Cuál de estas fracciones es mayor?

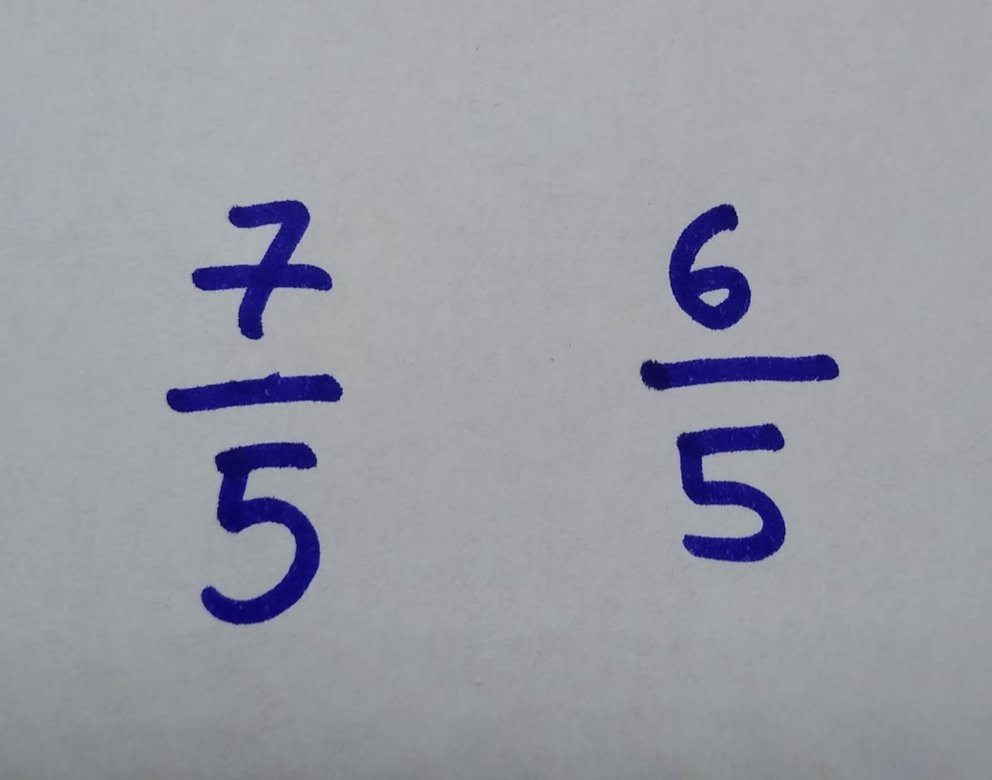
Desde la medida, ambas representan cantidades de magnitud. Las dos utilizan subunidades del mismo tamaño, quintos de unidad. Es mayor 7/5 porque he tomado 7 subunidades en lugar de 6. Gráficamente, queda muy claro.

Desde el reparto. 7/5 representa la cantidad de, por ejemplo, tortilla que recibe cada participante en un reparto de 7 tortillas para 5 personas. En el otro reparto hay menos tortillas y son las mismas personas. Por lo tanto, 7/5 es mayor, porque reciben más cantidad.

Una diferencia entre el modelo de medida y el de reparto es que el primero hace referencia a acciones físicas (particionar la unidad, tomar tantas subunidades, etc.), mientras que el de reparto suele ser siempre más evocado.

Vamos con estas. Muchos alumnos van directos a hacer común denominador. ¿Really?

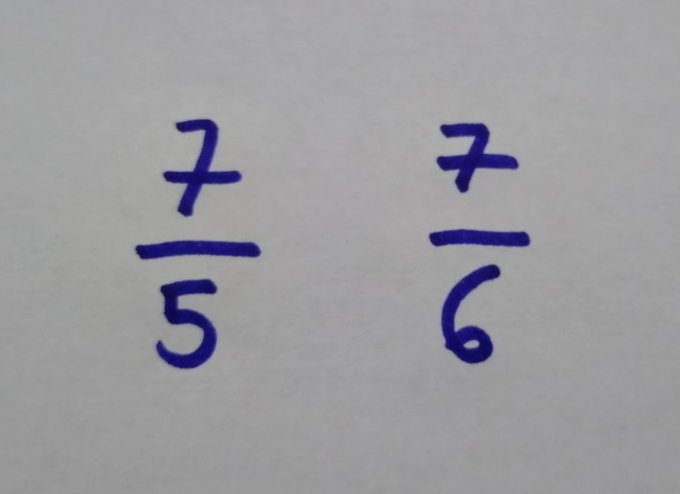
Desde la medida. En ambas fracciones tengo el mismo número de subunidades. Pero en una he dividido la unidad en 5 para hacer mi subunidad, y en la otra en 6. Son mayores los quintos porque he dividido mi unidad en menos partes iguales. Por lo tanto, es mayor 7/5.

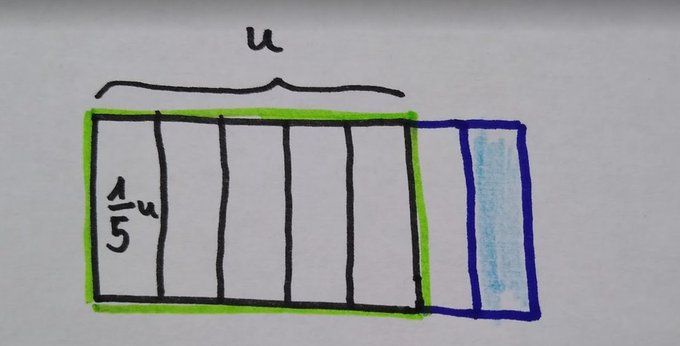
Gráficamente también se ve muy bien. En verde, remarco la unidad de medida (ver hilo de la multiplicación unpacked).

Desde el reparto. En ambos repartos estoy repartiendo el mismo número de tortillas. Lo que ocurre, es que en uno hay 5 participantes y en otro hay 6. Reciben más cantidad los que participan en el 7 para 5.

¿Y si estamos en este caso? ¿Cuál será mayor? ¿Común denominador y nos lo quitamos de encima? Vamos a ver qué opciones tenemos.

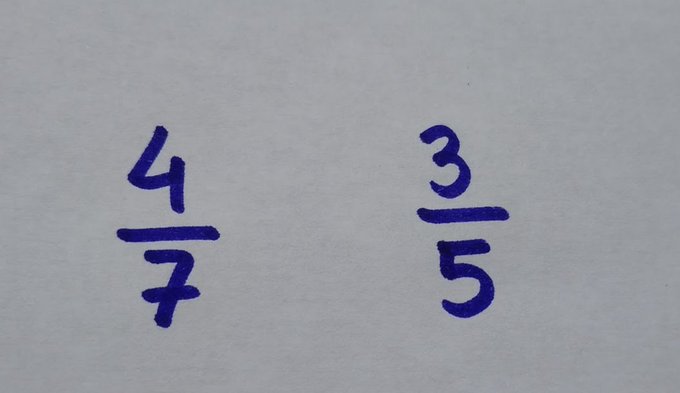
Desde la medida, podríamos ver que ambas son un poquito mayores que media unidad. También, que a la primera le faltan 3/7 para la unidad y a la segunda 2/5. En fin, no sé, la primera son más subunidades pero más pequeñas.

Y gráficamente, o lo hago con precisión o con alguna aplicación o no está claro. Desde luego, con mis dibujines no salimos de dudas. ¿Lo hacemos con una app y ya? No. Mejor poner sobre la mesa que no está claro.

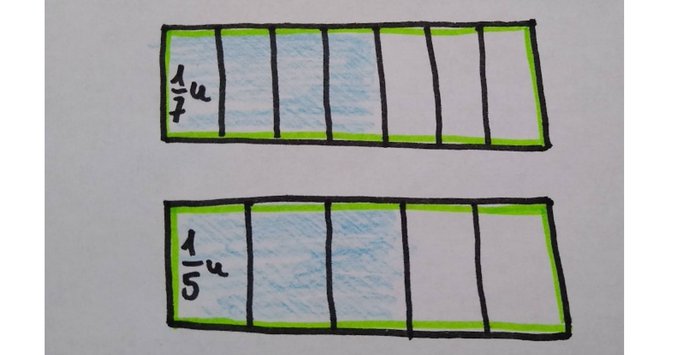
Tenemos que echar cuentas. Desde la medida podemos tratar de igualar el número de subunidades o igualar el tamaño de estas. Empecemos por el procedimiento más familiar: igualar el tamaño de subunidades.

4/7 u expresa la misma cantidad de magnitud que 20/35 u. Lo único que he hecho es tomar 5 veces más subunidades, las cuales son 5 veces más pequeñas (he partido en 5 los séptimos). 3/5 expresa la misma cantidad que 21/35. Por lo tanto, 3/5 es mayor. Sí, esto es común denominador.

Pero si os fijáis no hablo de numerador y denominador (que solo indican una posición en la notación, arriba y abajo), hablo en términos de medida. Y bueno, la equivalencia se habrá trabajado previamente. Vamos a hacerlo ahora igualando el número de subunidades.

4/7 u expresa la misma cantidad de magnitud que 12/21, mientras que 3/5 u expresa la misma cantidad de magnitud que 12/20. Al dividir la unidad en 20 partes iguales obtengo subunidades que son mayores que los que resultan al dividirla en 21. Por lo tanto, 3/5 es mayor.

Desde el reparto. También de dos maneras, puedo igualar el número de objetos a repartir o el número de participantes.

Igualo el nº de participantes. El reparto 4 para 7 es equivalente al 20/35, pues los participantes reciben la misma cantidad. Vamos, que hay 5 veces más tortillas y estamos 5 veces más personas. El 3/5 es equivalente al 21 para 35. Comeremos más en el 21 para 35. 3/5 es mayor.

Igualo el nº de tortillas. El reparto 4/7 es equivalente al 12/21, ya que hay el triple de tortillas y somos el triple de personas. Por lo mismo, el 3/5 es equivalente al 12/20. Comemos más en el 12/20, pues hay el mismo nº de tortillas, pero hay una persona menos. 3/5 es mayor.

Perdón por dejar la pregunta gancho para el final. Vamos con esto de aquí. Claro, no puse suma ni nada. Solo preguntaba que qué sugería. En el hilo de ayer hubo quien decía que le sugería un error muy común al tratar de sumar fracciones.

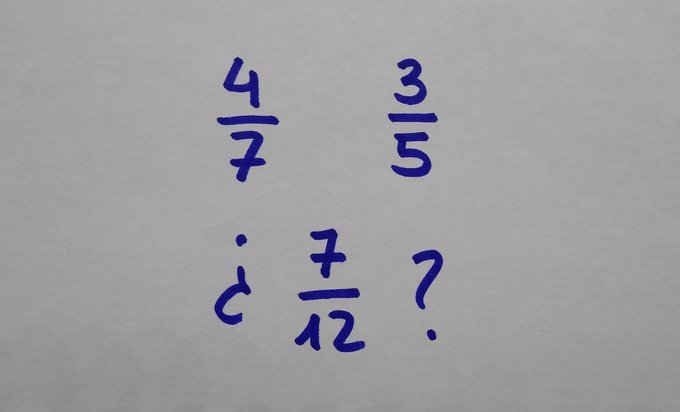
Estos errores, dificultades específicas aparte, suelen tener su origen en que no disponen de un modelo sobre el cual reconstruir lo que está pasando. Se aprenden unas reglas formales y ya. Si eres espabilado, pues vale. Si no, pues mal. Y en cualquier caso, es hacer malabares.

Desde el modelo de reparto, ¿qué significado tiene hacer (4+3)/(7+5)?

Antes de seguir, trata de imaginarlo.

En efecto, es un nuevo reparto en el que juntamos las tortillas de los dos repartos originales (pasamos a tener 7 tortillas) y juntamos los participantes (pasamos a estar 12).

Imaginaros que en una fiesta de cumpleaños, en la sala A, están los del 4/7. Y en la sala B, están los del 3/5. Ya sabemos, por lo de antes, que a los de la sala B les toca más tortilla.

Pero oye, resulta que se conocen y deciden juntarse. ¿Quién sale mejor parado en el nuevo reparto?

Los de la sala A, que tocaban a menos, ahora recibirán más cantidad de tortilla. Mientras que los de la sala B, que tocaban a más, recibirán menos cantidad. Es lo que tiene la socialización.

El reparto socializado está entre medias de los dos originales. Por eso, 7/12 es una fracción intermedia entre el 4/7 y el 3/5. Y si quiero buscar más fracciones intermedias, no tengo más que repetir el proceso. Por ejemplo, 11/19 es mayor que 4/7 y menor que 7/12.

Para encontrar fracciones intermedias, tanto desde el modelo de medida como en el de reparto, habríamos podido amplificar. Es otra técnica. Resumo. Ya sabemos que 4/7 es equivalente a 20/35 y que 3/5 lo es a 21/35. La primera a su vez es equivalente a 200/350 y la otra a 210/350.

De ahí podemos sacar varias fracciones intermedias.

Por el camino, además, está la idea de densidad de los números racionales. El significado parte-todo no permite lo esencial, que debería ser asumir que estamos ante un nuevo conjunto numérico.

Todo esto está desarrollado en el fantástico libro «Números y algoritmos» de Gairín y Sancho. Estas cosas las trabajamos dentro de la asignatura Didáctica de la aritmética II en FacultadEducaUZ.

Vuelvo a etiquetarlo con #cosicasdeDAII para que lo encuentren mis alumnos.