Por qué las coordenadas geográficas van «al revés» y algunas implicaciones didácticas

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

Por qué las coordenadas geográficas van «al revés» y algunas implicaciones didácticas.

Spoiler: no van al revés de nada.

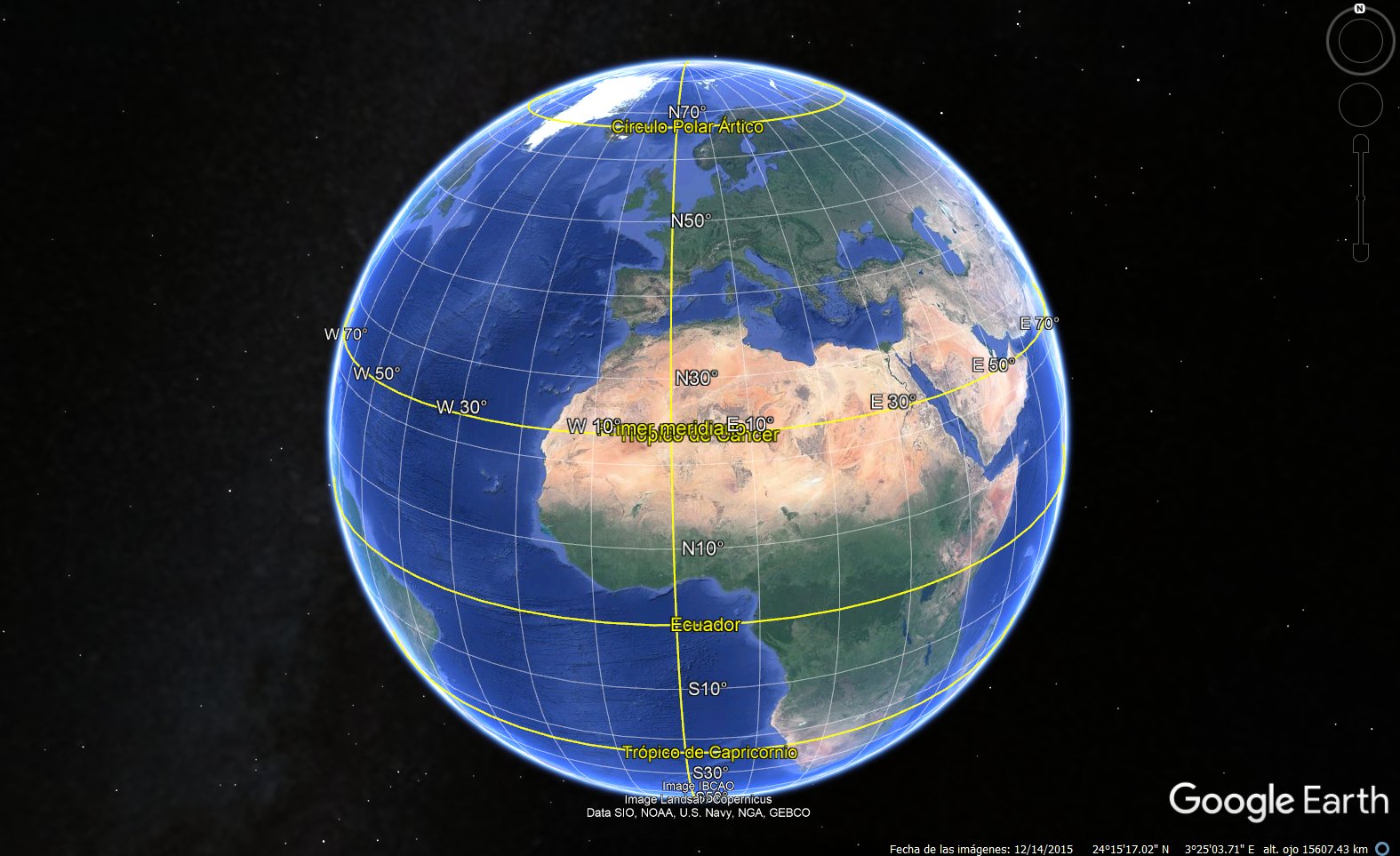
¿Cómo localizamos puntos en la superficie terrestre? Con las coordenadas geográficas, que indican latitud y longitud.

• Ea, pues ya está, como x e y. Abscisas y ordenadas. Horizontal y vertical.
• Esto… no.

¿Qué es la latitud de un punto de la superficie de la Tierra? Imagina una recta que pase por dicho punto y el centro de la Tierra. El ángulo que forma dicha recta con el plano ecuatorial es la latitud. Por eso va acompañada de una N (si es hacia el Norte) o una S (Sur).

Cualquier punto del ecuador se corresponde con el paralelo 0°, el polo norte con 90°N y el polo sur con 90°S.

¿Y qué es la longitud? Ahora toca imaginar meridianos (semicircunferencias que pasan por el polo norte y por el polo sur). Se elige uno de referencia, el de Greenwich, y la longitud de un punto es el ángulo entre ese meridiano de referencia y el que pasa por este punto.

En la imagen, la latitud es el ángulo Φ y la longitud es el ángulo λ.

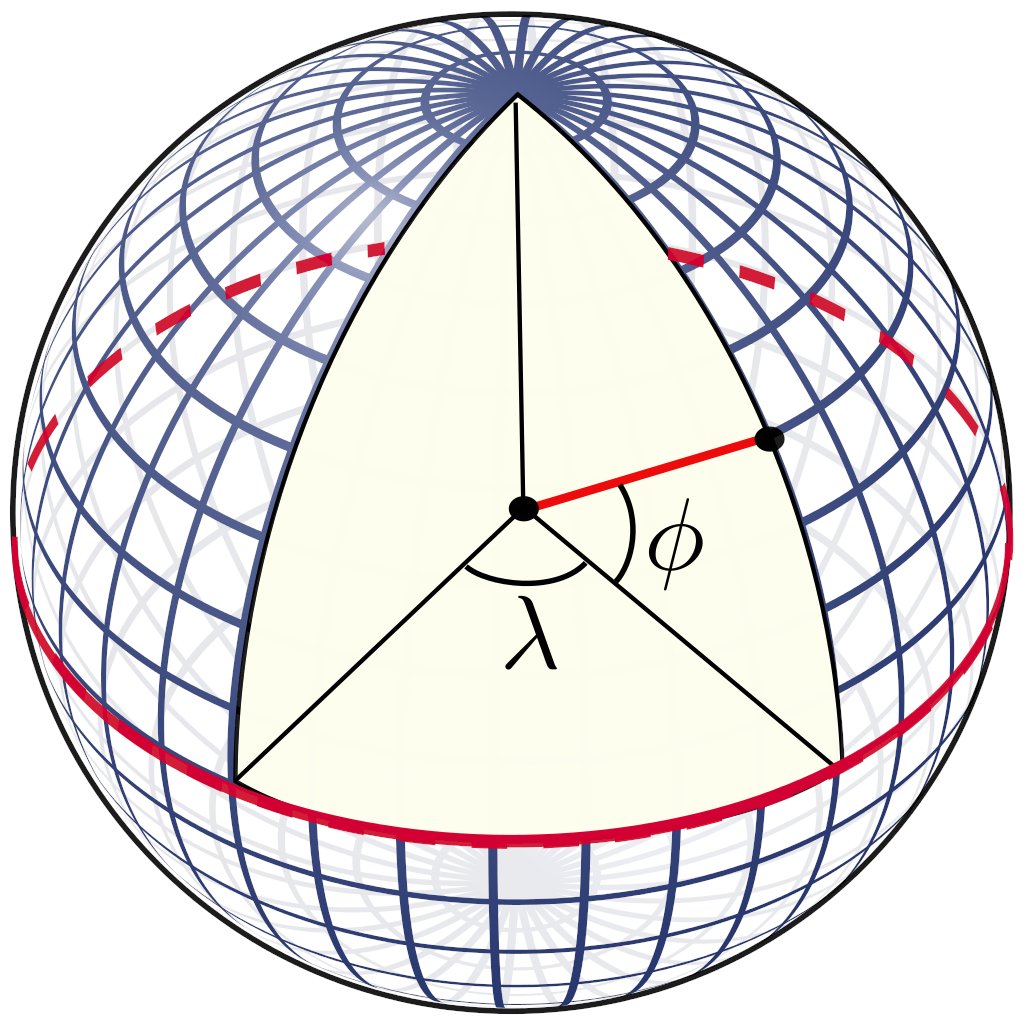
Medir la longitud es mucho más complicado que medir la latitud. Pensad que sois navegantes del s. XVI. Es más fácil percibir que te desvías hacia el Norte o hacia el Sur que en términos de longitud (E-O). Problemón que llevó al desarrolló del cronómetro y otros instrumentos. Enlace al museo virtual del CSIC

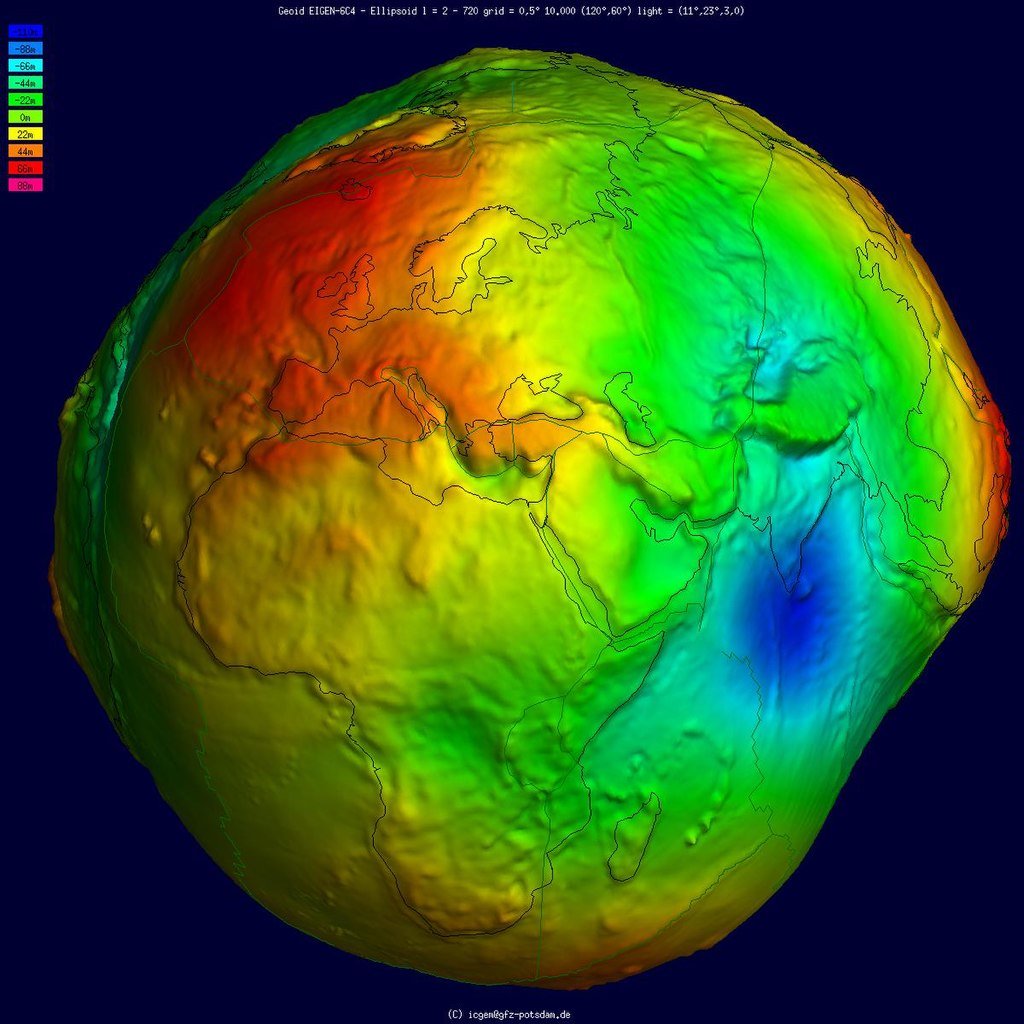
Además, resulta que la Tierra no es una esfera, sino un esferoide, por lo que podríamos añadir la altitud sobre el nivel del mar a nuestro sistema de coordenadas. Pero no lo liemos más.

📷ICGEM

Un alumno, o cualquier persona, puede pensar que las coordenadas geográficas van «al revés» porque primero se indica la latitud (Norte o Sur) y luego la longitud (Este u Oeste). Y claro, como Norte es arriba y Sur es abajo, ya la tenemos liada.

Ya la tenemos liada porque, en matemáticas, [modoironíaON], como todo el mundo sabe, eje X es horizontal y eje Y es vertical. Y los puntos en el plano son (x,y).

En el currículo nacional aparece esto de las coordenadas como contenido en Ciencias Sociales:

• Coordenadas geográficas: latitud y longitud.

Con su criterio «Identificar y manejar los conceptos de paralelos, meridianos y coordenadas geográficas» y su estándar «Localiza diferentes puntos de la Tierra empleando los paralelos y meridianos y las coordenadas geográficas.»

En Matemáticas aparece como contenido esto:

• Sistema de coordenadas cartesianas. Descripción de posiciones y movimientos. Y un estándar que dice «Describe posiciones y movimientos por medio de coordenadas, distancias, ángulos, giros.»

Para mi gusto, aparece muy ligada la idea de sistema de coordenadas cartesianas a la descripción de posiciones y movimientos, lo cual es un uso de los ejes. ¿De dónde salen los convenios en los ejes? ¿Cuáles son? ¿Cómo los usamos para representar cantidades de magnitud?

Mucha tela que cortar, como el problema de restringir la ‘x’ y la ‘y’ como etiquetas exclusivas. ¿Y si son ‘e’ y ’t' ya no son ejes cartesianos?

Todo esto se aborda con suma delicadeza en el librito del Shell «El lenguaje de funciones y gráficas». Os lo descargáis de aquí: https://sede.educacion.gob.es/publiventa/el-lenguaje-de-funciones-y-graficas/pedagogia/1065

Por ejemplo, si queremos hacer reflexionar al alumnado acerca de todo esto de los ejes, vamos a ponerles la altura en el eje horizontal.

Volviendo a lo nuestro, si el objetivo es comprender el concepto de coordenada geográfica, la secuencia didáctica no puede empezar con un mapa plano. Hemos de empezar con un globo terráqueo. Solo así quedará claro que para localizar un punto utilizo ángulos.

La cuestión es que claro, no vamos con un globo terráqueo en el bolsillo. Hoy en día casi, porque usamos el móvil y dispositivos que lo permitirían. Observa que cuando queremos presentar en 2D el globo terráqueo se produce una deformación. Probadlo con el Google Maps.

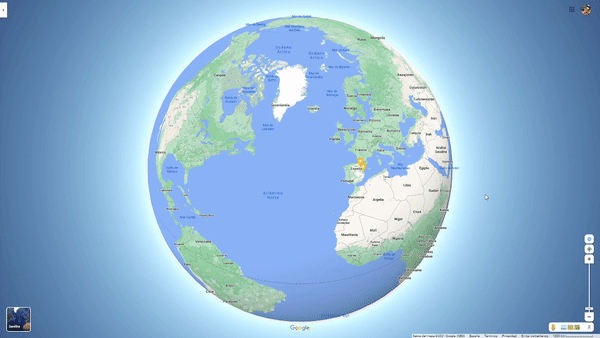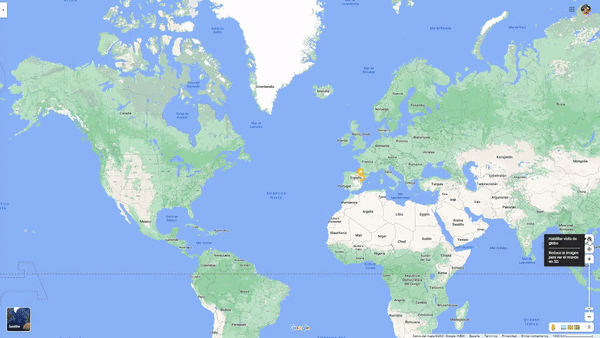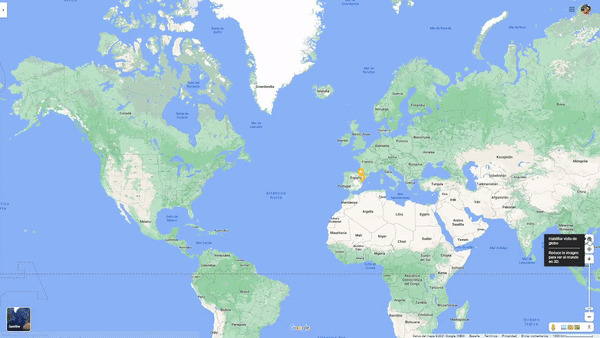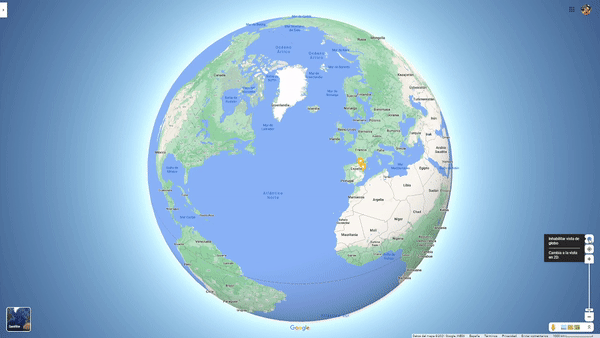
Estas deformaciones son diferentes según el tipo de proyección que se realice. Y unas conservan unas cosas y otras, otras. Paralelismo, perpendicularidad, distancias, áreas, etc. Enlace sobre tipos de proyecciones

Lo importante, si nos acercamos a esto en primaria, es comprender que necesito indicar los ángulos de latitud y longitud para localizar un punto. Que por convenio se suela decir antes la latitud es lo de menos. Eres igual de capaz de localizarlo si te doy la información al revés.

Ahora, si reduzco la secuencia didáctica a localizar puntos en un plano 2D a partir de latitudes y longitudes, pues igual no hace falta hacer nada.

Gracias @Jaimetimiraos por la conversación de esta mañana, donde me señalabas este posible conflicto.