Sobre las matemáticas que se hacen estos días en casa

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

Coincido con la lectura que hace Lynne McClure @clm4d de la situación a la que nos ha llevado el coronavirus en @CambridgeMaths: Home truths about mathematics

Traduzco libremente a la vez que comento y pongo ejemplo de actividad.

Y es que percepción que tiene @clm4d es que se está poniendo el énfasis en que el alumnado haga en casa lo que se “supone” que deberían estar haciendo en la escuela:

• Formularios con preguntas tipo, orientados a algún examen.
• Ejercicios mecánicos de respuesta cerrada, proporcionando abundantes ejemplos del mismo tipo.
• Tareas centradas en grabar lo que hacen en lugar de explicar y describir.

Dejando aparte la cuestión de que todo esto no debería ser el núcleo del trabajo habitual de aula, Lynne señala que, precisamente ahora, hay una oportunidad para intentar algo diferente (y mejor).

Una oportunidad para estudiantes de todas las edades para experimentar, con calma y a su ritmo, lo que significa pensar matemáticamente, ser creativo, “ensuciarse” con un problema.

Esto es posible con muy pocos recursos. Dados, peonzas, papel, tijeras, tapones… se puede explorar, estimar, predecir y hablar sobre lo que piensa cada uno en cada una de esas situaciones.

Lynne termina proponiendo alguna actividad de @nrichmaths, como Dotty six y Got it!. Ayer, @javiarrospide compartía un documento recopilando y traduciendo alguno de estos juegos. 😍

Por otro lado, Lynne llama a la tranquilidad recordando algún ejemplo donde esta forma de trabajar no deja en desventaja a los alumnos frente a una forma de trabajar más “formalista”.

De hecho, esa pregunta que me hacen a veces, me parece falaz.

• ¿Y qué pasa si al curso que viene les lleva un profesor que no trabaja así? Bueno, pues es que es peor al revés. Aunque de esto ya hemos hablado alguna vez, podemos volver a sacar el tema otro día.

Así que gracias @clm4d por compartir esa reflexión. Por otro lado, ayer recibimos aquí en Aragón las instrucciones actualizadas. Me gustan bastante, aunque no se mojan en la evaluación final que, entiendo, es todavía un tema peliagudo.

Aunque tardar en decir lo inevitable ocasiona una angustia innecesaria. Las instrucciones hablan de seleccionar contenidos, de evaluar para adaptar los futuros procesos de enseñanza y aprendizaje.

Os cuento algo que hemos mandado a los de 1º y 2º de ESO. Es una actividad basada en una práctica que hacemos en @dm_unizar, sobre las áreas de las figuras planas. Dejo en este enlace la ficha para descargar.

En esos cursos, es algo que ya han trabajado, normalmente limitándose al aprendizaje de las fórmulas ☹️. En esta tarea se introduce la idea de polígonos equivalentes y se les pide que se olviden de esas fórmulas (de las que se acuerden, claro…).

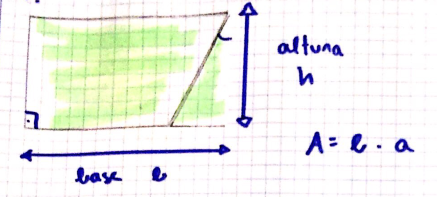
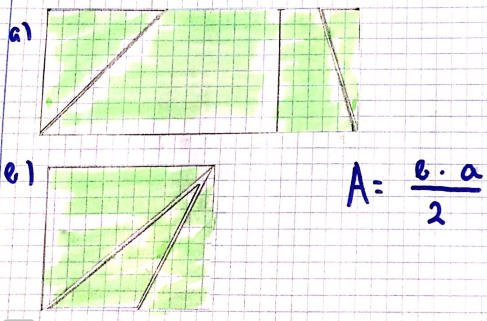
Se trata de coger las tijeras y convertir esas figuras en un rectángulo equivalente, con el mismo área, de forma que se pueda deducir la fórmula del área. Aquí, producción de una alumna para el paralelogramo y los triángulos (esta última se les ha atragantado a muchos).

Les hemos hecho dos vídeos (hablo en plural porque mi compi y yo decidimos compartir aula virtual):

• Uno para el primer día, dedicado a los que no leen el enunciado o no se aclaran, introduciendo la del paralelogramo.
• Otro, ya con muchas entregas realizadas, comentándolas. “Igual” que hacíamos en clase, donde este curso apenas estaba usando ya la pizarra. Por ejemplo, en las que he mostrado antes falta indicar qué son b y a en la figura original. Es decir, falta la conexión entre esas áreas.

Es una pena enorme no hacer esta actividad en clase, porque da para una sesión y pico, y puedes llegar a conectar con el área del círculo (cosa que aquí hemos quitado) e, incluso, con áreas de figuras cualesquiera. Aquí, podada, la hemos propuesto para una semana.

No es que se pierdan la explicación, porque no hay explicación, salvo una pequeña institucionalización al final. Es que se pierden todo el proceso de exploración en conjunto y discusión de diferentes soluciones, uso de vocabulario, etc.

Les hemos propuesto que hablen entre ellos, claro, pero no es lo mismo. Ni de lejos. Luego, además, están los que no pueden conectarse, los que no tienen las mismas facilidades, los que se la copian y ya, etc.

Creo que es un ejemplo de algo que tocaba ver este año, pero que todos “conocían” ya. Permite trabajar explorando y fomenta la autonomía. En algún momento hablaba de enriquecimiento horizontal, refiriéndome a este tipo de cosas.

Y nada más, que quería compartir esto por aquí. Hacer esto a distancia no es guay, es un parche de los gordos. Pero va en la línea que comentaba Lynn, y la que pienso que piden las instrucciones. Ya está.