El caso del número que al multiplicarlo por 45 da 555555555

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

Multiplica el número 12345679 por 45. Va hilo con actividad maja para ~5ºEP-2ºESO.

Ahora, multiplica 12345679 por 27.

¿Qué observas?

Bueno, pues aprovechando que peque mayor (5ºEP) se ha prestado, os comento. Esto es lo que sale la primera (luego comento sobre el algoritmo).

Y esto es lo que sale la segunda multiplicación.

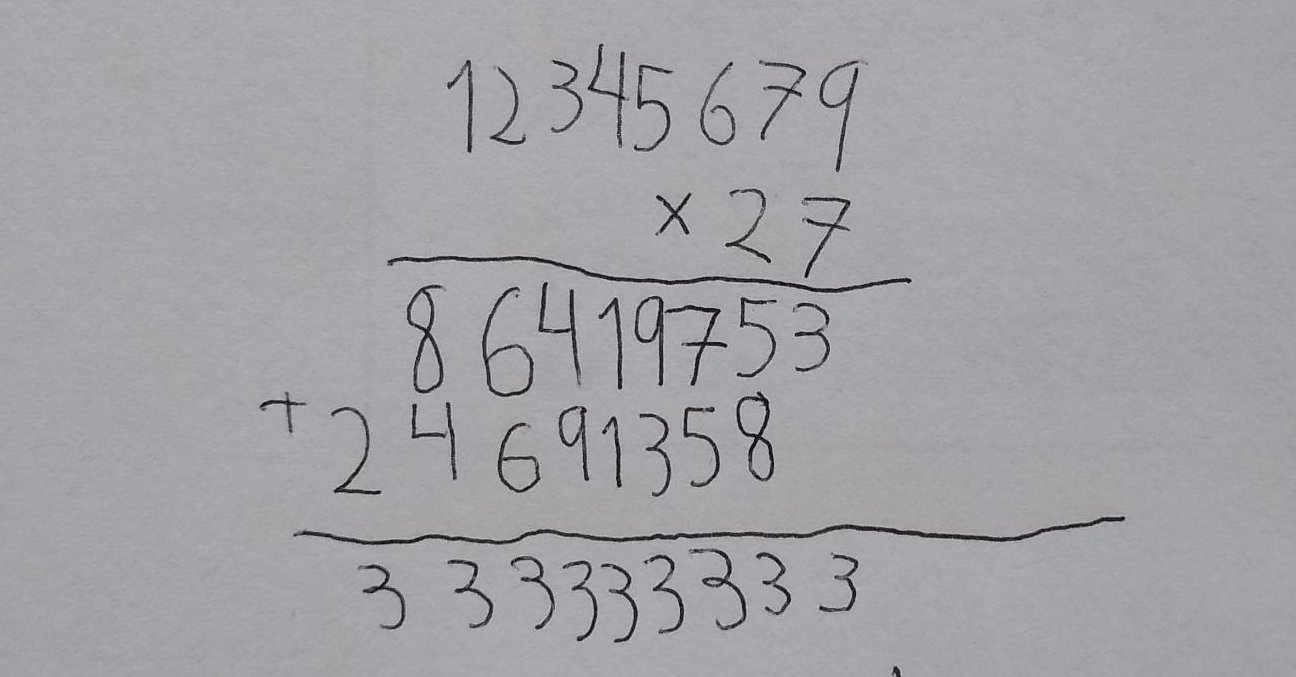
Amazing, ¿verdad? ¿Qué observas? Tómate tu tiempo, que luego viene lo que viene.

¿Qué observas? Si es que hasta me lo ha escrito…

Nota de clase: no hacer spoilers. Cosas como esta, salen. La mejor forma de trabajarlas, dejarlos en grupos de cuatro.

Preguntas.

• ¿Y por qué número he de multiplicar para obtener todo doses? ¿Y todo ochos?

Aquí la respuesta de peque mayor.

Efectivamente, por 18. Aquí le he invitado a usar la calculadora, que estaba por la mesa.

• Vale, ¿y para obtener todo 8 ochos?
• Pues por 72.

• ¿Es posible obtener números formados por todo 1, todo 2, todo 3, … todo 9?
• Sí… vamos a ver.
• Pero compruébalo, eh.
• Todo 1, por 9. Todo 2, por 18. Todo 3, por 27…

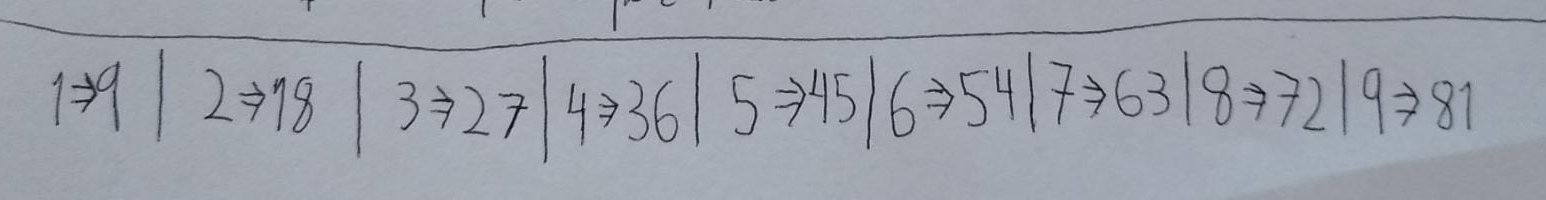
Hasta aquí hemos conjeturado. Y hemos comprobado todos los casos. Sin embargo, ¿por qué ocurre esto?

Al principio, me ha repetido lo de bajar una unidad y subir otra.

• Mmm, pero eso es lo que has hecho para construir esos números, no es una razón para que funcione, ¿no? ¿Qué más observas?

Realmente, antes de esta pregunta ya había observado que todo eran múltiplos de 9. Ahora es cuando ha vuelto a ver que si para sacar todo 1 se multiplica por 9, para sacar todo 2 habrá que multiplicar por el doble (18, que es el siguiente múltiplo…).

Cuando lo he hecho en clase sale también la cuestión de las factorizaciones, que realmente es decir lo mismo con otro lenguaje.

$45=5\times 9$.

Por lo tanto, si $12345679 \times 9=111111111$, $12345679 \times 9 \times 5 = 555555555$.

Había prometido que hablaría sobre los algoritmos de los tuits iniciales. Ni le he dicho de hacerlos a mano ni cómo. Como veníamos de hacer el otro día esta otra actividad

Me ha preguntado si podía hacerlo como quería, y le he dicho que sí. Ahora bien, al final le he preguntado si tener los algoritmos ahí delante le ha ayudado con sus observaciones o no. Es decir, si se había fijado en ellos o no.

• No, lo de cada fila no tiene nada que ver…

De hecho, esta actividad la vi hace tiempo en la Guía Praxis, aunque está recogida en más sitios. Y se propone directamente con calculadora. Porque aquí el algoritmo no aporta nada.

Con este hilo he querido mostrar, por un lado, una actividad sobre «la multiplicación» y sus cositas asociadas. Por otro, contrastar el objetivo con el de la del otro día, la de hacer el algoritmo de izquierda a derecha, que también era rica, pero diferente.

Alejados de la vida cotidiana TM

Ayer escribí un hilo sobre una actividad para hacer en clase de matemáticas que, en realidad, está muy alejada de la «vida cotidiana» TM. Es puramente intra-matemática. ¿Cómo se motiva al alumnado para hacer esto?

Si esperáis una receta mágica, aquí no la encontraréis. PERO.

Me atrevo a sintetizar el asunto en las siguientes claves:

1. Que estas tareas se planteen sobre los significados personales de los alumnos. Es decir, sobre lo que ya conocen los alumnos, no sobre lo que se supone que saben. Insisto, sobre lo que conocen y cómo lo conocen.

Para eso es indispensable que el trabajo parta de ellos. Por esta razón, en algún momento del hilo hablaba de que estén en grupos de cuatro, de puestas en común, etc.

De esta manera los significados se «negocian», en lugar de «imponerse». Y esto quiere decir que se construyen. Es eso lo que permite que el aprendizaje sea significativo (por esto hablo en este hilo de significado) y no si el contexto (o decorado) es de la vida cotidianaSigno de marca registrada o no.

2. Que la cultura de aula tenga integradas este tipo de tareas, donde aunque las preguntas iniciales puedan parecer tontorronas, sepan que siempre hay algo más. Ese tipo de tareas no hace falta disfrazarlas de nada.

Estos cambios en la cultura de aula no llegan de un día para otro. Siempre lo digo. Esa resistencia, además, no es cosa mía, está recogida en la literatura científica sobre el tema. Y la solución, que no receta mágica, pasa por mostrarse coherente.

Así que, respondiendo a la pregunta inicial, no se motiva a los alumnos de ninguna forma específica para realizar esa tarea. Lo que se busca es la motivación intrínseca.

Y bueno, en la búsqueda de esa coherencia, ayuda mucho, especialmente, la evaluación. Pero eso es otra historia, sobre la que ya hemos hablado alguna vez, y seguiremos haciéndolo.