Los materiales educativos concretos no son drogas milagrosas

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

Vamos con una #DidMatCita (y mini hilo) sobre el uso de materiales manipulativos. Siempre hay que tener presente una cosa, que a veces se olvida: “Los materiales educativos concretos no son drogas milagrosas. Su uso productivo requiere planificación y previsión.” (Szendrei, 1996)

Y es que ya van dos veces, recientemente, que veo experiencias con regletas de Cuisenaire que me hacen torcer el morro. Experiencias que ponen el énfasis en la asociación color-número. Es decir, blanco=1, rojo=2, y así.

Szendrei (1996), precisamente, pone las regletas de Cuisenaire como ejemplo de material manipulativo con gran potencial que, en muchas ocasiones, se utiliza mal o de forma poco adecuada.

Estas regletas son un buen recurso para desarrollar la idea de medida y, a partir de ella, aprender conceptos numéricos y de operaciones. No obstante, aquí lo fundamental es la medida. De hecho, permiten introducir la idea de fracción desde esta rica perspectiva.

No solo eso, sino que también se han mostrado muy útiles para trabajar conceptos de series, funciones y ecuaciones, para formular conjeturas y ayudar a guiar la intuición. Con estas tareas, además, nos acercamos a la idea de prueba en matemáticas.

Todo esto se fundamenta en algo muy básico. Y no es otra cosa que en no hacer una asociación única entre colores y números. Porque el mal uso de estas regletas nace cuando se fuerza a los alumnos a memorizar la convención número-color.

Esta asociación conduce a la realización de tareas triviales de sumas, de manera que las regletas pasan de ser un recurso para el aprendizaje a ser un contenido en sí mismas.

Otro mal uso se produce cuando en las primeras actividades con regletas , el profesor utiliza la regleta blanca llamándola “unidad”. Posteriormente, se miden el resto de regletas y los niños aprenden que la roja es el dos, la verde claro el tres, y así.

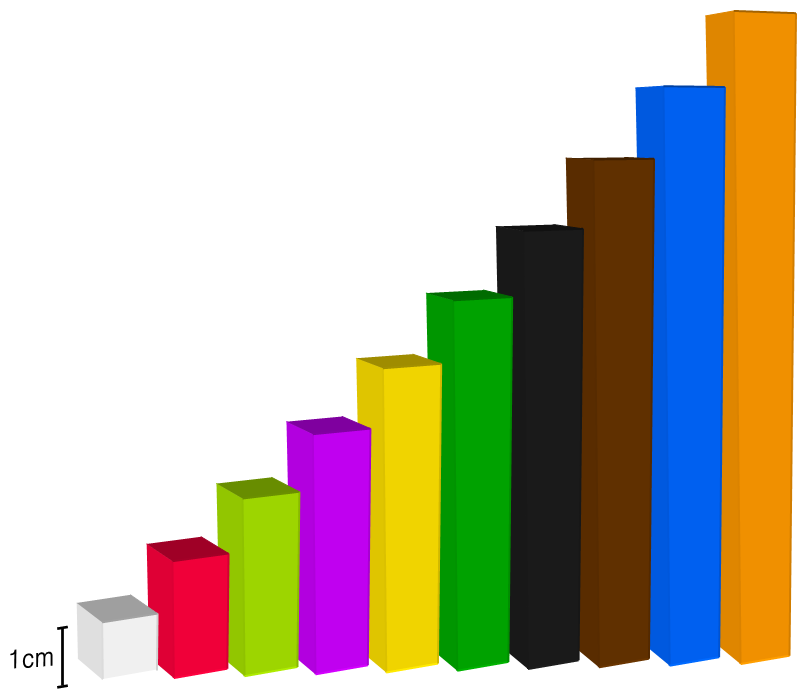
Las actividades que siguen a continuación dan la impresión de que los alumnos suman y restan con facilidad usando las regletas. Esto conlleva dos grandes problemas. Por un lado, los alumnos aprenden una asociación sin significado, color-número.

Por otro lado, se crean la concepción, errónea, de que una longitud es un número. Si bien al comienzo pueden decir que la longitud de la roja es dos veces la de la blanca, muy pronto comienzan a decir que la roja es el dos o la amarilla el cinco.

En particular, este proceso genera obstáculos muy serios de cara al aprendizaje de las fracciones. Los alumnos que han sido forzados a utilizar la blanca como unidad, no comprenderán más adelante que no importa qué regleta sea la unidad.

Ahí es donde pueden escuchase cosas tan extrañas como que “ahora el amarillo va a ser el uno”, en lugar de decir que “la longitud de la regleta amarilla (o la que mide 5 cm) será la unidad de medida”.

Szendrei termina señalando que, si bien hay manipulables muy sencillos, hay otros que requieren de un curso para ser usados de forma adecuada. Y esto concuerda con la necesidad de formación en didácticas especificas.