Más sobre la regla de tres

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

En este caso, de nuevo, recomiendo fervientemente bucear entre los comentarios.

Ha vuelto a hablarse mucho de la regla de tres esta semana. Ocasión que aprovecho para escribir un poquito más sobre el asunto. Prometo que incluyo novedades respecto a episodios anteriores.

No es que esté obsesionado con el asunto particular de la regla de tres. O sí y me lo tengo que hacer mirar, yo qué sé Cara de loco. Tan solo es que me parece algo paradigmático. Lo que me quita realmente el sueño es el aprendizaje mecanicista e instrumental de las matemáticas.

Ñeñeñe, cómo que las matemáticas no son instrumentales. Mira, no vivo en burbuja. Ya sé el papel que juegan en otras disciplinas y en la vida cotidiana (y en esto último está sobrevalorado). Sin embargo, centrarse en lo instrumental es una receta para el desastre.

Pero eso es otra historia que debe ser contada en otra ocasión. A lo que íbamos, esta semana me animé a plantear un hilo interactivo, donde animaba a compartir problemas «de regla de tres», que me tuvo muy entretenido. Más de la cuenta, quizás, aunque sarna con gusto, no pica.

El hilo fue muy interesante porque aparecieron problemas de valor perdido o faltante, tentativas de comparación (donde no procede la regla de tres y sigue siendo proporcionalidad), repartos, pseudoproporcionalidad (que no tienen sentido), etc.:

Recuerdo que la regla de tres es una técnica que encuentra su justificación en las reglas del álgebra. Es decir, la justificación es sintáctica. $\cfrac{a}{x} = \cfrac{b}{c} \Rightarrow x = \cfrac{a \cdot c}{b}$

El «este por este entre este» sale de ahí.

• Pues ya está, ¿no?
• Pues no.

El caso es que los problemas «de regla de tres» son aritméticos. Y una característica esencial de la aritmética es que el control no es sintáctico, sino semántico. Es decir, radica en el significado de los números que intervienen. En cada momento.

He puesto problemas «de regla de tres» entre comillas porque técnicamente se conocen como de valor perdido o faltante (missing value problems). Es decir, se trata de encontrar uno de los cuatro valores de la proporción. No son los únicos problemas de proporcionalidad.

Están los de comparación, por ejemplo, donde no vale la regla de tres. O situaciones donde no tenemos números.

Entre las interacciones, aparecen variantes de esto:

• No, es que siempre hay que comprobar si se puede aplicar. Con eso ya estaría evitando esa ilusión de linealidad.
• ¿Comprobar el QUÉ?

Para los nuevos, la ilusión de linealidad consiste en creer que una relación es de proporcionalidad cuando no lo es. El aprendizaje mecanicista basado en técnicas tipo producto cruzado o regla de tres la fomenta.

Lo fomenta por mucho que nos hagamos la pregunta, ¿es directa? ¿es inversa? Lo de comprobar si se puede aplicar se las trae. En primer lugar, para comprobar algo primero hemos de haberlo CONSTRUIDO. Y eso pasa por caracterizar muy bien a qué llamamos relación de proporcionalidad.

En lo que sigue me centraré en la proporcionalidad directa. La proporcionalidad inversa es un objeto muy alejado matemáticamente y daría para otro hilo. De todas formas, mucho de lo que comento aquí es, en esencia, extrapolable.

COMPROBAR. El qué.

• ¿Que a doble de una tengo doble de otra? ¿Y a triple?
• ¿Que a más, más, y a menos, menos? Esos argumentos como caracterización no valen. Pueden servir, una vez CONSTRUIDO el modelo en matemáticas, para ver si es sensato para estudiar un fenómeno físico.

Esa construcción es delicada y lo que está detrás como idea matemática es el significado del número racional. La proporcionalidad nos ofrece, quizás, el más abstracto de todos los objetos de la aritmética escolar.

Pensemos en los números naturales, que ya son abstracciones. Cuando «repartimos» una cantidad de magnitud entre otra para obtener una razón, esa razón es un nuevo tipo de objeto, con un nivel mayor de abstracción. Simboliza una relación. Aparece una nueva magnitud.

Si para una receta de limonada echo 3 litros de zumo por cada 10 de agua, puedo calcular las siguientes razones: 3/10 (tres décimos o 0,3, que son otras representaciones de dicha razón) y que significa los litros de zumo que echo por cada litro de agua.

10/3 de litro de agua que echo por cada litro de zumo. Aún podrían obtenerse más razones, como la cantidad de zumo por litro de limonada. O al revés. Bien, el caso es que el 3/10 es una cantidad de una nueva magnitud que no aparecía en el texto de la situación.

A veces, estas nuevas magnitudes tienen nombre propio. Cuando digo que María corre 10 km en 50 minutos, 10/50=1/5=0,2 es velocidad. Los km que recorre en cada minuto. Al revés, 50/10= 5 sería ritmo, minutos que tarda en recorrer un km.

Por supuesto, para poder hacer esas divisiones tengo que asumir una «condición de regularidad», sino no tiene sentido ni plantearla. En el caso de la limonada, que siempre se eche la misma cantidad de zumo por cada litro. Sobre esto ya he hablado en otros hilos.

A fin de cuentas, esta abstracción se traduce en verbalizar el significado de las razones implicadas (decir qué significa una «división»). Es muy importante, porque claro, luego están las conexiones que aparecen con funciones, análisis y con álgebra.

Vaya por delante que la aproximación vía el uso de estas razones ya es mucho más potente que la regla de tres para situaciones cotidianas. Si no lo piensas es porque te enseñaron así. Hay gente plenamente funcional a la que no se la enseñaron. Luego volvemos a esto.

Cuando nos vamos a identificar la relación de proporcionalidad desde funciones y gráficas, vuelve a aparecer el concepto clave que conecta todo, en este caso. La razón, tal y como la hemos introducido antes.

La representación gráfica de una relación de proporcionalidad directa es una recta que pasa por el origen. ¿Y su pendiente?

Si no quiero reducir todo a una serie de ejercicios triviales, tendré que recurrir a darle significado, para además conectar con los conocimientos previos. Y aquí entra en juego el significado del racional como razón.

Significado que la regla de tres no desarrolla porque directamente lo ignora. Por lo tanto, si no lo he desarrollado y quiero conectar con esa idea, ¿qué? A ver, que el significado de estas cositas no se construye por arte de magia. Exige una planificación y cierta coherencia.

Esta idea de pendiente, razón… se conecta, mirando hacia el álgebra, con la constante de proporcionalidad. Y mirando hacia el análisis, con la tasa de variación media. Concepto sobre el que sustenta la derivada. ¿Vamos con los cimientos bien asentados?

Por supuesto, en el hilo ha habido quien detecta esta eliminación de la regla de tres como un ataque. Tanto docentes como familias. En este último caso, en un tuit me dicen que eliminemos lo que queramos, que en casa seguirán enseñando la regla de tres.

Aquí tenemos un problema de creencias, que se puede sintetizar en algo así:

• A mí me enseñaron la regla de tres y aquí me tienes. No será tan mala. Además, la uso para todo. Controlo perfectamente cuándo se puede usar y cuándo no.

La divulgación en este sentido ha de ser cuidadosa y respetuosa. Lo mismo que en clase, no se trata de prohibir la regla y ya. Es cuestión de enfocarlo dando significado. Y que la evaluación sea coherente con lo que se hace.

Creo que pensar que el objetivo de fondo no es resolver un tipo concreto de problema, sino estudiar un tipo de relación y desarrollar el significado del racional como razón, ayuda.

Cuando terminé de responder a los problemas planteados en el hilo interactivo, me dio por poner este problemita.

https://twitter.com/pbeltranp/status/1448405548924293129

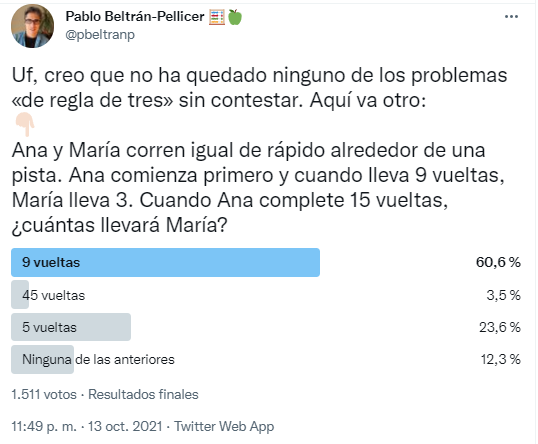
Se trata de la traducción de un problema utilizado por Cramer et al. (1993), quienes lo propusieron a una muestra de 33 futuros docentes de educación primaria.

32 de los 33 futuros docentes emplearon la proporción: 9/3 = x/15; 3x = 135; x = 45. Cabe observar que este problema es perfectamente resoluble, no como otros de pseudo-proporcionalidad (si hay 10 médicos en la planta 2, ¿cuántos habrá en la planta 5?).

De Bock et al. señalan que la cuestión con el problema de las corredoras es que se presenta en el formato clásico de un problema de valor faltante («de regla de tres»). Eso ocasiona que esta situación aditiva se interprete como multiplicativa.

En mi encuesta gana la opción correcta de 9 vueltas. Pero casi la cuarta parte opta por decir 5 vueltas, resultado que se obtiene aplicando la regla de tres o una estrategia multiplicativa.

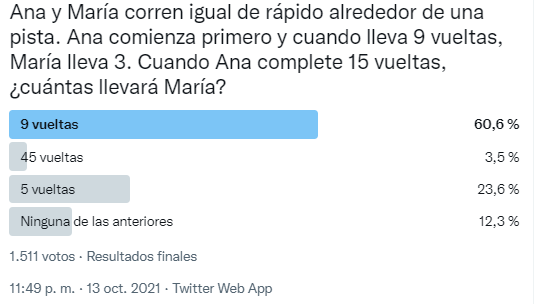
La diferencia con el estudio original, donde casi todos contestaban 45 vueltas, puede tener que ver con el idioma o con la forma de plantear la regla o el producto.

Y nada más, que vaya turra. Más hilos como este, o con secuencias didácticas, en mi perfil. Sí, si os sabe a poco este, tengo alguno más sobre la regla de tres, proporcionalidad y número racional.

Epílogo 1

Como os habéis quedado con ganas, me parece muy pertinente este hilo de @RadiactivoMan. Realmente, el tema de la modelización en experimentales lo he mencionado ya, pero aprovecho para escribir un poquito más.

La modelización en matemáticas y experimentales sigue caminos opuestos. En matemáticas se construye y se abstrae ese modelo ideal, mientras que en experimentales se utiliza para predecir y conocer más de lo sensible.

Al hilo de lo que dice @RadiactivoMan, en experimentales se comprueba si el modelo matemático se ajusta o no a cierto fenómeno y bajo qué condiciones.

Tengo un PERO importante con respecto a los factores de conversión. Son muy fáciles de aplicar (tacha, tacha, tachán) y, de nuevo, ocultan la relación de proporcionalidad que hay detrás de, en muchos casos, un simple cambio de unidades.

Verbalizar esa relación, aunque cueste más, da un mayor control de lo que se está haciendo. Vamos, que no se trata de despejar de aquí y de allá, entiendo, sino de comprender a fondo cómo es la relación entre esas magnitudes.

Además, el uso de esos factores da la sensación de que el alumno en cuestión sabe lo que está haciendo. Cuando a lo mejor solo le interesa que “cuadre”.

Epílogo 2

Nada, como veo que hay quien se interesa por esto, aquí va una referencia fácil de leer de un clásico como Skemp sobre las matemáticas instrumentales y las relacionales.

Un saludo y… ¡feliz clase!