El problema de contar cubitos

Nov 18, 2018 2 min de lectura acrimates, secundaria, primaria

Es muy, pero que muy importante conectar registros y representaciones diferentes de un mismo objeto matemático. Por registros entendemos el registro verbal natural, el gráfico, el simbólico-numérico, el simbólico-algebraico, etc. Por representaciones, por ejemplo, diferentes expresiones algebraicas equivalentes. O diferentes gráficos sobre un mismo problema.

Voy a dejar aquí el material para llevar a cabo una sesión de visualización de descomposición de números, con sus factorizaciones y sus potencias (descargables al final). Se trata del problema de contar cuántos cubos pequeños faltan para completar el cubo grande. A partir de este problema, para lo que me he inspirado en el libro de Problemates de Lluís Segarra (de hecho, la primera configuración que se plantea es exactamente la misma que aparece en el libro).

La tarea

Antes de realizar la tarea que propongo en esta sesión, es preferible haber realizado alguna más de visualización de operaciones, como la que muestro en la imagen de cabecera. Con los policubos, o regletas, o cualquier otro material, se trata de componer números y escribir las operaciones que conducen a ellos. Viendo que, precisamente, el dos al cubo se llama así porque…¡es un cubo!
Nota: las configuraciones las he dibujado con esta herramienta del NCTM, enlace que he compartido con ellos y que hemos usado en clase para ayudar con la visualización.

Vamos a contar cuántos cubos pequeños faltan para completar el cubo grande

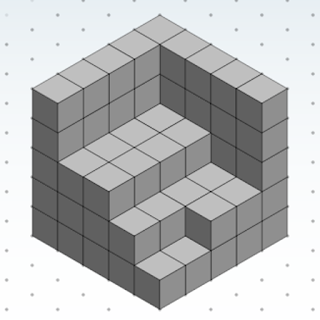
Dejamos tiempo. De hecho, yo lo propuse como tarea para el siguiente día. Y algunos alumnos consiguieron ver que faltaban 42 cubitos, pero otros no. Así que la siguiente sesión comenzó mostrando una posible visualización, prestando especial atención a la expresión aritmética que representa esa forma de contar.

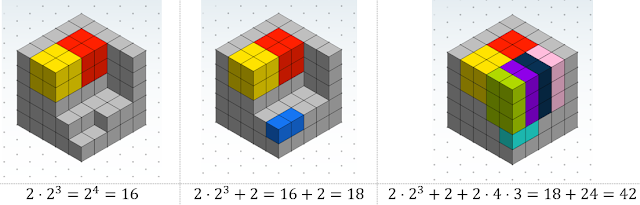
Y después, la ficha con la tarea. Hay que pintar sobre cada una de las configuraciones y escribir en el recuadro la expresión correspondiente. También les entrego una hoja con un geoplano isométrico para la segunda parte. Conviene observar que esta tarea es un ejemplo claro de atención a la diversidad, cosa que no siempre conseguimos. Los alumnos que visualizan con más facilidad, tienen que buscar más expresiones para una misma configuración. Por ejemplo, contando los que hay en lugar de los que faltan.