Una introducción a Desmos
La utilización de las TIC en nuestras clases puede responder a diversos propósitos. Estando claro que no hay que introducirlas porque sí, podemos distinguir entre herramientas generalistas, como Moodle o Edmodo, de carácter organizativo; o Kahoot, con el que se consiguen interacciones de aula que pueden resultar atractivas de cuando en cuando. Sin embargo, la dinámica de uso de todas estas herramientas es la misma sea cual sea la materia. Me explico, da lo mismo si estamos enseñando historia, lengua, música o matemáticas. O lo que sea. Sin desdeñar estas herramientas (soy el primero en usarlas), siento más interés por otras que sí que afectan en cómo aprenden nuestros alumnos. En los significados que adquieren. El ejemplo más claro en matemáticas es Geogebra. Esta entrada la voy a dedicar a otro software con elementos de geometría dinámica, Desmos, que también añade la posibilidad de plantear secuencias didácticas muy interesantes. Vale, algunas de ellas pueden llevarse a cabo sin TIC, como el polígrafo, sí, pero Desmos lo facilita mucho. Y otras conjugan la potencia de la geometría dinámica con discusiones de aula muy ricas.
¿Qué es Desmos?
Realmente, Desmos se compone de diferentes aplicaciones:
- Una calculadora gráfica.
- Una calculadora con cuatro campos de entrada que se pueden relacionar de forma interactiva.
- Una calculadora científica.
- Una herramienta de geometría dinámica.
Sin embargo, el factor diferenciador de Desmos son las actividades y secuencias didácticas que ofrece, ya preparadas para su utilización y edición. Comentaremos a continuación las más TOP.
Las canicas
Supongamos que echamos un vistazo a la lista de las actividades más populares y que elegimos Marbleslides: Lines. La descripción inicial indica la duración aproximada (45-60 minutos) e incluye una breve explicación y se clasifica a las actividades por tipos: introducción, desarrollo, para practicar o para aplicar. Marbleslides: Lines es una actividad de desarrollo, con la que los estudiantes pueden profundizar en lo que significan los parámetros de la ecuación de una recta, o cómo expresar restricciones en el dominio de estas. En este caso nos encontramos con una guía para el profesor, imprimible y que refleja una serie de buenas prácticas y consejos para pautar la actividad:

Aquí, por ejemplo, se señala la conveniencia de comenzar con lenguaje matemático informal e ir incorporando poco a poco respuestas más formales. En otras palabras, puede decirse que el diseño de la actividad tiene en cuenta el proceso de negociación de significados que caracteriza, por ejemplo, al aprendizaje basado en problemas. Es a partir de las tareas propuestas que emergen los objetos matemáticos considerados en los contenidos. El significado de estos objetos difiere según las situaciones, pero también varía entre los individuos y las instituciones de referencia. Así, ante una fracción como 3/4, un alumno puede estar pensando en los 3 trozos que se ha comido de una tarta dividida en 4 partes; mientras que otro directamente piensa en 0,75; y el docente puede estar pensando en el número racional. El diseño de las secuencias didácticas en Desmos reserva momentos para evaluar estos significados personales, permitiendo negociarlos a través de las sucesivas tareas.
El mecanismo es similar al de otras aplicaciones, como Kahoot. Creamos un código de clase para la actividad y, a partir de ese momento, al docente le aparece un enlace en su lista de actividades para gestionar la misma a través de su dashboard. Este código es el que tienen que introducir los estudiantes en https://student.desmos.com, aunque también se genera un enlace que conduce directamente a la instancia de la actividad. Si los alumnos están registrados en Desmos, podrán volver a la sesión más adelante, pero no es un requisito.
En Las canicas, todo un manipulable virtual, los alumnos deben modificar la expresión de una recta, añadir otras rectas o definir restricciones a un nuevo dominio, de manera que consigan crear un circuito de canicas para que estas pasen por unos puntos predefinidos de antemano por medio de unas estrellitas. Realmente, se puede trabajar esta actividad con rectas o parábolas, ya que tenemos Marbleslides: Lines y Marbleslides: Parabolas y, en cualquier caso, el programa no restringe la función a utilizar.
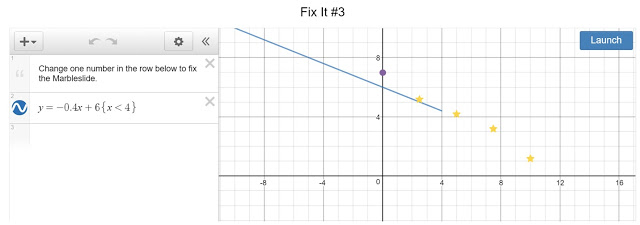
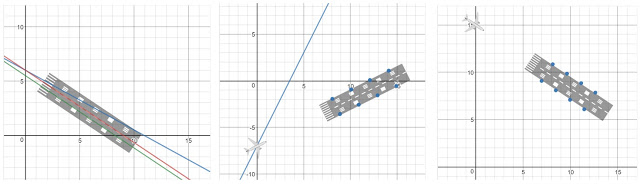
Por ejemplo, en la Figura 2 basta con extender el dominio, definiendo la función para x<6 en lugar de para x<4, para que la fuerza de la gravedad haga su trabajo y la canica llegue a pasar por la estrellita que está en las cercanías del punto (10,1). Esta solución se muestra en la figura anterior, a la izquierda, y la expresión que hay que introducir es la siguiente:
$$y=-0.4x+6\left\{x<6\right\}$$
Sin embargo, otros alumnos podrían haber planteado:
$$y=-0.4x+6\left\{x<10\right\}$$
$$y=x-9$$
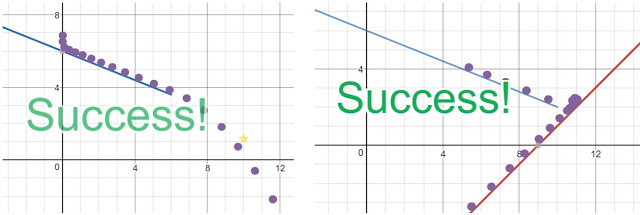
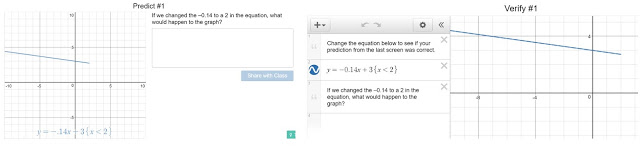
No todas las tareas que componen la actividad son iguales. En las primeras pantallas se proporciona la expresión de alguna función lineal y únicamente hay que cambiar algún parámetro. En las siguientes pantallas se trata de predecir lo que ocurrirá si se cambia el parámetro indicado y de comprobarlo. Las respuestas de los estudiantes pasan a estar disponibles para todos los demás, de manera que cuando llega la puesta en común, todos están al corriente de lo que han puesto los compañeros que han llegado antes a esa tarea. Las últimas pantallas son retos (challenges) en los que los alumnos deben introducir las expresiones que consideren oportunas.
El escritorio del profesor (dashboard) ofrece información para gestionar el desarrollo de la secuencia. De esta manera, el profesor puede observar el avance de cada uno de los alumnos (o parejas, si lo estamos haciendo por pequeños grupos). Además, puede detener la actividad para las puestas en común o momentos de institucionalización.
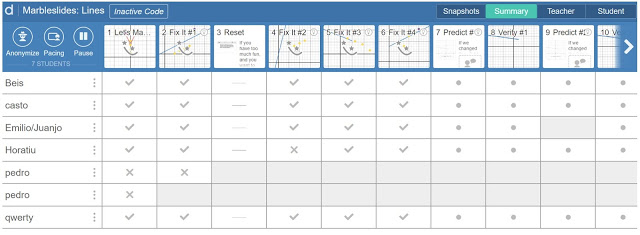
Aterrizando el avión (Landing the plane)
Al igual que las canicas,esta actividad forma parte del linear bundle, una secuencia más extensa sobre funciones lineales. Aquí se trata de encontrar la ecuación de la recta que representa la trayectoria óptima para el aterrizaje de un avión. Las primeras pantallas se dedican a explorar el entorno o implican cambiar únicamente algún parámetro, mientras que más adelante se ofrece menos guía al alumno y se plantean cuestiones para la reflexión.
El polígrafo
Se trata de un quién es quién en toda regla y es una de las actividades más populares en Desmos, siendo fácilmente editable. De hecho, esto último es la gran ventaja que ofrece respecto a la versión física. Hay polígrafos subidos por otros profesores sobre los más variados contenidos (una búsqueda en septiembre de 2018 devuelve nada menos que 56 polígrafos). La siguiente captura de pantalla es del polígrafo de parábolas. Al igual que el quién es quién, se juega por parejas. Es decir, un ordenador para un estudiante o pareja y otro para otro. Conforme se van registrando los alumnos en la actividad, la propia plataforma los va emparejando para jugar. Se juega por turnos, de manera que una vez es un estudiante el que tiene que adivinar el objeto oculto, haciendo las preguntas necesarias. Estas cuestiones deben formularse de forma que se puedan responder con un sí o un no.
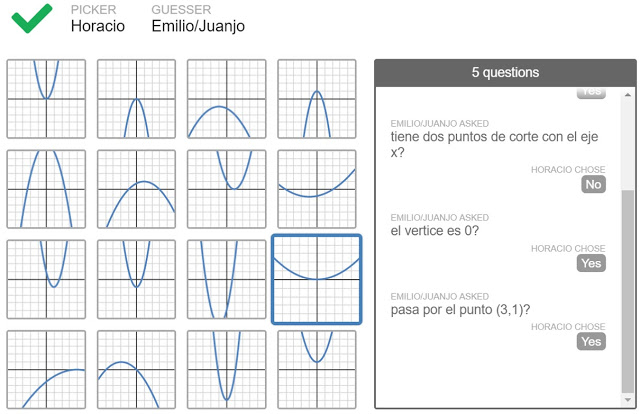
Los polígrafos son una excelente actividad de introducción, ya que permiten evaluar el conocimiento previo del alumnado, qué términos emplean, cómo describen los objetos matemáticos, etc. Por otro lado, también se pueden utilizar como actividad de desarrollo. No en vano, en el linear bundle, en el que se enmarcan la actividad de las canicas y la del avión, se incluyen dos polígrafos, uno como actividad de introducción y otro como desarrollo.
Representando historias gráficamente (Graphing stories)

Esta actividad está inspirada en la madre de todos los recursos para el aprendizaje de las funciones. Bueno, puede que exagere. O no. Me estoy refiriendo al librito de Swan (1985) titulado The language of functions and graphs, del* *Shell Centre. Hay una versión traducida por Alayo (1990), *El lenguaje de funciones y gráficas, *publicada por el Ministerio de Educación que se puede descargar gratuitamente.
Si en el libro de Swan aparecen circuitos de carreras y otros ejemplos a los que hay que asociar o crear una gráfica, en este caso el valor añadido radica en que se trata de vídeos. Este hecho, junto con la posibilidad de ir representando gráficamente la función que describe cada situación según avanza el vídeo, aumenta el rango de contextos y situaciones que podemos utilizar en la enseñanza y aprendizaje de las funciones.

Las tareas que contempla la secuencia, por otro lado, no se limitan a representar cada función, sino que antes de ello se incluyen preguntas para detenerse en las magnitudes involucradas, las unidades de medida apropiadas, etc.
Unos comentarios finales
Aunque el diseño de estas actividades está específicamente pensado para ser llevado a cabo en el aula con la guía del profesor, bien sea con portátiles, dispositivos móviles o en una sala de informática; también es posible asignar actividades de Desmos como tareas para casa. Esto es algo que tiene sentido, por ejemplo, con las actividades para practicar. Algo que solo hemos mencionado por encima es que Desmos permite que los usuarios (profesores) suban modificaciones a muchas de las actividades por defecto y otras nuevas. No resulta complicado modificar actividades ya existentes. Para ello, en la propia web hay bastante material de ayuda.
Dejamos para otra ocasión la experiencia de utilizar las funciones de edición avanzadas de Desmos. Al igual que hace Google con su Google Labs, al marcar las opciones de Desmos Labs accedemos a funcionalidades en estado beta que, en este caso, permiten crear tus propias Marbleslides, utilizar la herramienta de geometría en el constructor de actividades e, incluso, utilizar la capa de computación, con la que se puede utilizar un lenguaje de programación para diseñar actividades más sofisticadas.
Referencias
Beltrán-Pellicer, P. (2018). Una introducción a los tipos de actividades que podemos encontrar en Desmos. Entorno Abierto, Boletín Digital de la Sociedad Aragonesa «Pedro Sánchez Ciruelo» de Profesores de Matemática, 24, 4-10.