Algunas limitaciones del modelo parte-todo (tarta) a tener en cuenta
Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.
El significado parte-todo del número racional positivo no tiene un origen histórico natural. Vale, permite introducir de forma inmediata la representación fraccionaria, pero provoca graves limitaciones de comprensión. Vamos con #DidMatCita de Escolano (2007) e hilo.

Es evidente que toda génesis escolar de un tópico matemático es artificial y que no tiene por qué reproducir siempre el origen histórico, que puede utilizar constructos que hoy en día resultan extraños y complicados para nuestro alumnado. No es este el caso que nos ocupa.
Los modelos habituales utilizados ahora en la escuela para introducir los números racionales no solo son contradictorios con la historia de dichas nociones, sino que además no son una opción más económica desde el punto de vista didáctico, ni más cercana a las matemáticas de hoy.
Hoy nos centraremos en tres aspectos, creo, muy curiosos.
- ¿Cuándo surge el modelo parte-todo?
- ¿Por qué tiene un significado diferente al de medida?
- ¿Qué obstáculos genera?
Para responder, he seleccionado unos fragmentos de la propia tesis de Escolano.
«El origen de la enseñanza de la fracción con el significado parte-todo lo encontramos en la primera mitad del siglo XX, como consecuencia de la pérdida de la referencia del proceso de medida de cantidades de magnitud.»
Escolano se sirve de un libro de Edelvives de 1934 para ejemplificar el tránsito de la utilización de modelos de medida aparente al de relación parte-todo. Esto pudo venir de la mejora en las técnicas de impresión de libros, que pasan a incluir gráficos.
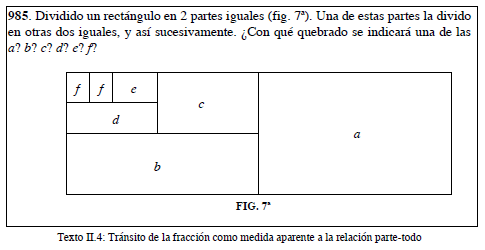
El caso es que en el período comprendido entre los años 1950 a 1970 la relación parte-todo se consolida como el método prioritario con el que se enseña la fracción. En 1962 se encuentra esta sugerencia en documentos oficiales de enseñanza:
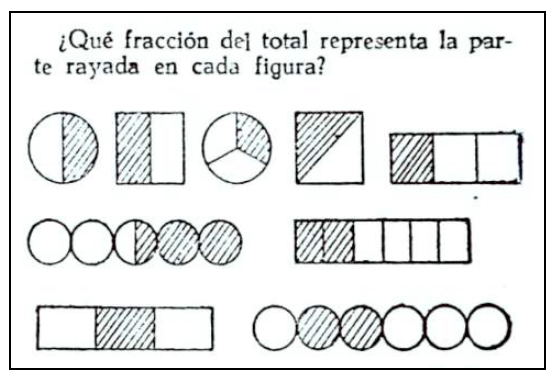
«En los enunciados se habla de “representar”, que invita al escolar a aplicar un convenio previamente establecido; no sugiere la realización de acciones, físicas o mentales, que favorezcan el aprendizaje autónomo.»
¿Por qué tiene el parte-todo un significado diferenciado?
Hay autores que lo han relacionado con el de medida. Por ejemplo, Behr (1986) señalaba que “el subconstructo medida del número racional representa una reconceptualización de la noción parte-todo de la fracción”.
Escolano señala que no tiene significado de medida, tanto por las exigencias cognitivas que exige resolver los problemas de cada uno de los campos como por las ideas matemáticas implicadas en las respectivas estrategias de resolución.
Tampoco tiene significado de razón. Ese doble recuento en que se basa el parte-todo impide definir una nueva magnitud, aspecto crucial en este significado.
Y no tiene, tampoco, significado de:
- Cociente partitivo. Porque no expresa el resultado de un reparto.
- Operador.
- Cociente indicado.
Escolano aporta razones para cada uno de estos casos, concluyendo que estamos ante otro significado. Más pobre.
Obstáculos que se generan y que serían evitables:
Se obstaculiza la formación de concepciones adecuadas de la fracción.
- No existen las fracciones impropias (esto ya lo apuntaba Freudenthal).
- Las fracciones son números no medida.
Kieren (1992) señalaba que el conocimiento que construyen de la parte-todo es inflexible y difícil de aplicar a la amplia gama de situaciones que organiza el número racional.
- El “todo” o unidad no es un número. No se explicita el sentido y funciones de la unidad.
Se obstaculiza la separación conceptual del número racional y del natural.
Como el parte-todo se basa en un doble recuento (uno para numerador y otro para denominador…), resulta que:
- La fracción está formada por dos números naturales. No se entiende como un nuevo tipo de número.
Y los decimales tampoco. ¿No os suena lo de “Profe, creo que está mal, me sale decimal?”
- Las relaciones y operaciones con números racionales tienen el mismo significado que en los números naturales. Y aquí no hay concepto de siguiente, sin ir más lejos.
Se obstaculiza la formación de ideas abstractas.
- Los conceptos son las técnicas o procedimientos asociados a los mismos. Si siempre se usa la misma técnica, se confunde lo uno con lo otro.
- Los contenidos útiles son los procedimentales. Se memoriza el algoritmo y… 🤦🏻♂️
Una propuesta
Para solucionar todo esto, se propone utilizar el modelo de medida y el modelo de reparto. Pero ya hablaremos más sobre el tema, que es apasionante. De momento…
Dejo enlace a la tesis de Rafael Escolano. Va con anexos. Y estos, con un pequeño tesoro: el material que se les dio a los alumnos

Los he puesto más de una vez. El libro «Números y algoritmos» (Gairín y Sancho) aborda también esta cuestión, para secundaria.
En este artículo, orientado a primaria (válido también como “secundarios”, se cuenta algo similar y está en abierto aquí
Referencias
Berh, M. J., Lesh, R., Post, T.R., & Silver, E. A. (1983). Rational number concepts. En Lesh & Landau (Eds.) Acquisition of mathematics concepts and processes (pp. 91-126). Academic Press, New York.
Escolano, R. (2007). Enseñanza del número racional positivo en Educación Primaria: un estudio desde modelos de medida y cociente. Tesis doctoral. Universidad de Zaragoza.
Kieren, T. E. (1992). Rational and fractional numbers as mathematical and personal knowledge: Implications for curriculum and instruction. Analysis of arithmetic for mathematics teaching, 323-371.