Elige tu propia aventura: un teorema célebre

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter. He aprovechado para eliminar alguna redundancia que siempre se me termina escapando al escribir en esa red, pero siempre quedará ese aroma a hilo. Por un lado, debo decir que me gusta el tipo de lenguaje que hay que emplear al escribir un hilo, porque obliga a ir al grano y sintetizar mucho. Sin embargo, por otro lado, también soy consciente de que es… peculiar.

Vamos con otro de los de elige tu propia aventura. Eres profe de mates y toca ponerse con «el teorema de Pitágoras», digamos en 2º ESO. Dos opciones:

A) $a^2+b^2=c^2$

B) Calcula el área de este cuadrado.

La opción A es propia de una enseñanza para la resolución de problemas. Presentas el teorema. Posiblemente, esperando que el alumnado se maraville ante un resultado tan maravilloso (lo es). Esa misma clase expones cómo aplicarlo para calcular distancias desconocidas.

Los problemas de aplicación que vengan después pueden ser más o menos interesantes. Sin embargo, ¿estaríamos tratando realmente el teorema de Pitágoras? ¿Qué implica este teorema como contenido? ¿Cómo se conecta con otros contenidos?

La opción B, que es la que desarrollaré, es una propuesta de actividades a través de la resolución de problemas. La principal diferencia con la A es que no se exponen las matemáticas, sino que se construyen con el alumnado.

Este vídeo está genial. Pero si empiezas con él, aunque haya indagación, es muy probable que la propuesta sea de tipo A. Por otro lado, el vídeo tiene su cabida en la B, pero más adelante. ¡Es un spoiler!

Si tienes muy claro que lo tuyo es la opción A, sáltate el hilo, porque con la B puedes estar casi dos semanas.

La secuencia de actividades se titula «Un teorema célebre». No me gusta adelantar acontecimientos. Ya bautizaremos el resultado al final. Si algún alumno conoce el teorema y las actividades empiezan a recordarle el asunto, no pasa nada.

• Sí, por ahí van los tiros, ya verás.

El punto central de la propuesta es explotar la idea de que el teorema de Pitágoras es una relación de áreas. La situación-problema será el cálculo del área de cuadrados cuyos vértices se ubican en los puntos de una retícula cuadrada (geoplano cuadrangular).

Tareas troncales a realizar

Primera tarea (razón de ser)

Esto es un cuadrado de tipo $(3,5)$. El primer número es el desplazamiento en horizontal que hacemos desde un punto fijo. El segundo, el desplazamiento en vertical. Y así tenemos un lado del cuadrado. Encuentra el área de este cuadrado y explica cómo lo has hecho.

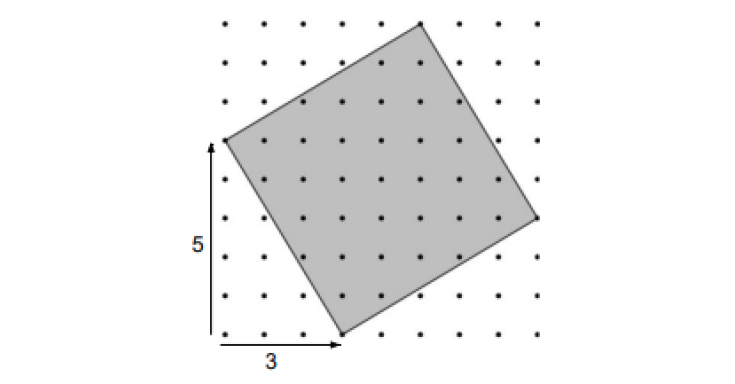
Ponte en la piel de alguien que no conoce el teorema de Pitágoras y prueba a contestar antes de seguir, porque aquí empiezan a pasar cositas. Desde alumnos que señalan que el lado del cuadrado mide 5 unidades hasta diferentes tipos de descomposiciones.

Inciso: lo de que mida 5 u el lado o contar puntos en lugar de «huequitos». No me cansaré de decir lo importante que es el trabajo en magnitudes y medida. Con 13-14 años no conservan la longitud. Y para eso están estas secuencias. Si quieres saber más visita este post sobre una secuencia en torno a la medida.

Esto es el suelo bajo de la secuencia (ya veréis que el techo es alto). ¿Por qué el suelo es «bajo»? Porque es accesible para todos. Esta tarea podría llevármela a 4º de primaria y trabajarla tranquilamente allí.

Es más, esta tarea forma parte del trabajo en magnitudes y medida que se esperaría hacer en primaria. Por lo que, aparte de ser suelo bajo, es una oportunidad para establecer conexiones con conocimientos previos.

En el caso de estos alumnos, las conexiones más cercanas son con cosas que hicimos el curso pasado durante el confinamiento. Por un lado, la actividad que se describe en este post, donde se trabajan descomposiciones y recomposiciones de figuras planas para hallar su área.

Y con una secuencia que hicimos después de la actividad anterior, en torno al teorema de Pick. Secuencia en la que, llegar al teorema de Pick casi es lo de menos. Empezaba pidiendo calcular las áreas de estas figuras.

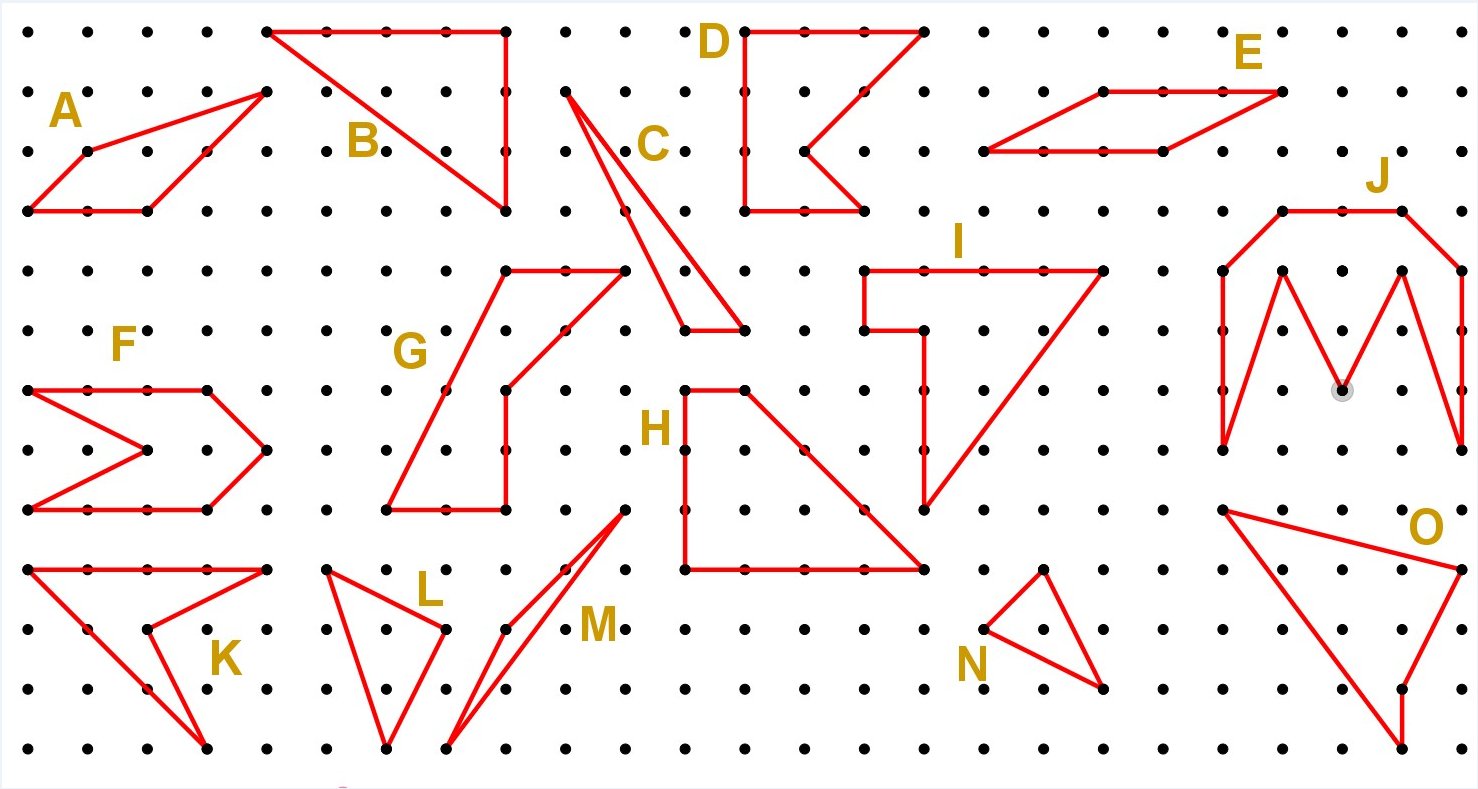
En clase normal habríamos discutido diferentes técnicas. En modo confinamiento, tal como lo planteamos nosotros, propusimos las siguientes:

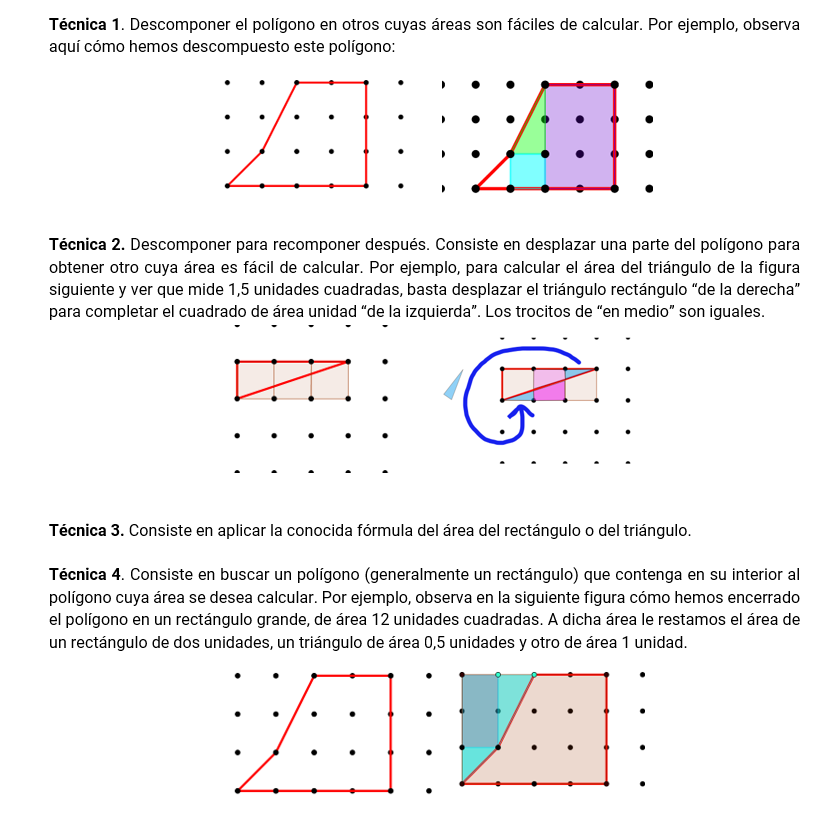
Creo que las conexiones con lo que estábamos planteando se ven claras, ¿verdad? Es posible que la secuencia de Pick no la haya desarrollado por aquí, así que me lo apunto 😉. Os dejo un avance:

Volviendo a nuestro «cuadrado inclinado» $(3,5)$. La forma más habitual de enfrentarse fue inscribirlo en otro más grande de área conocida y restar los sobrantes, que son fáciles de obtener.

Pero hay pequeñas variantes, como esta. E incluso otras, recomponiendo el cuadrado, que ya no muestro por no extenderme. En clase hemos de estar atentos y procurar discutir todas. ¿Qué observas? ¿Cuál es más fácil en este caso? ¿Se te ocurre otra forma?

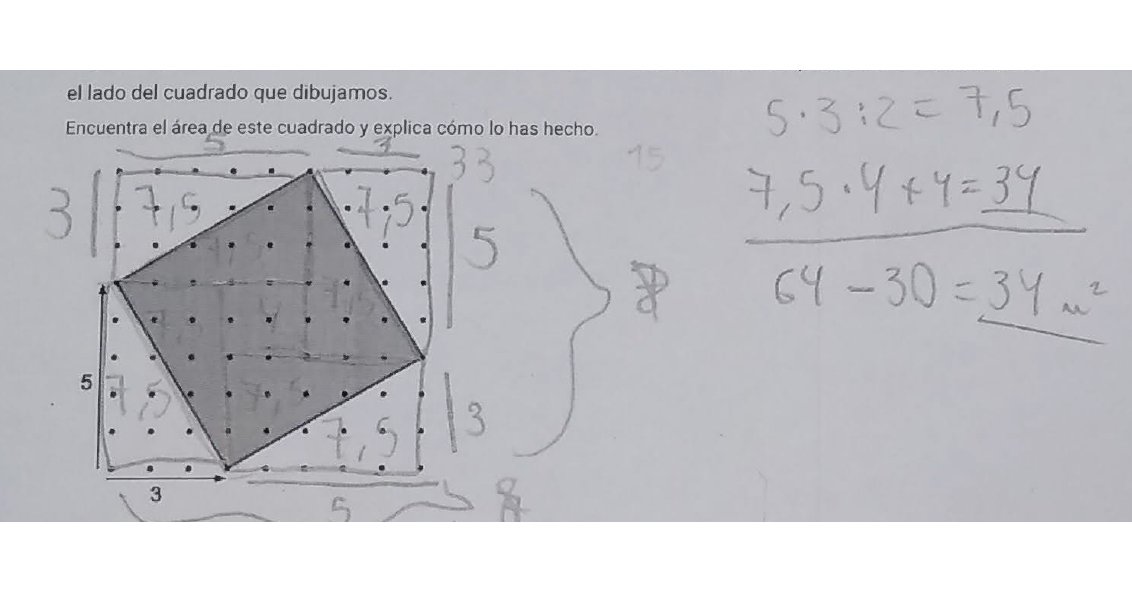
Siguientes tareas: hacia la generalización

Vamos a asegurarnos de que sabemos dibujar estos cuadrados inclinados y calcular el área. Hagamos el $(3,7)$ y el $(2,3)$.

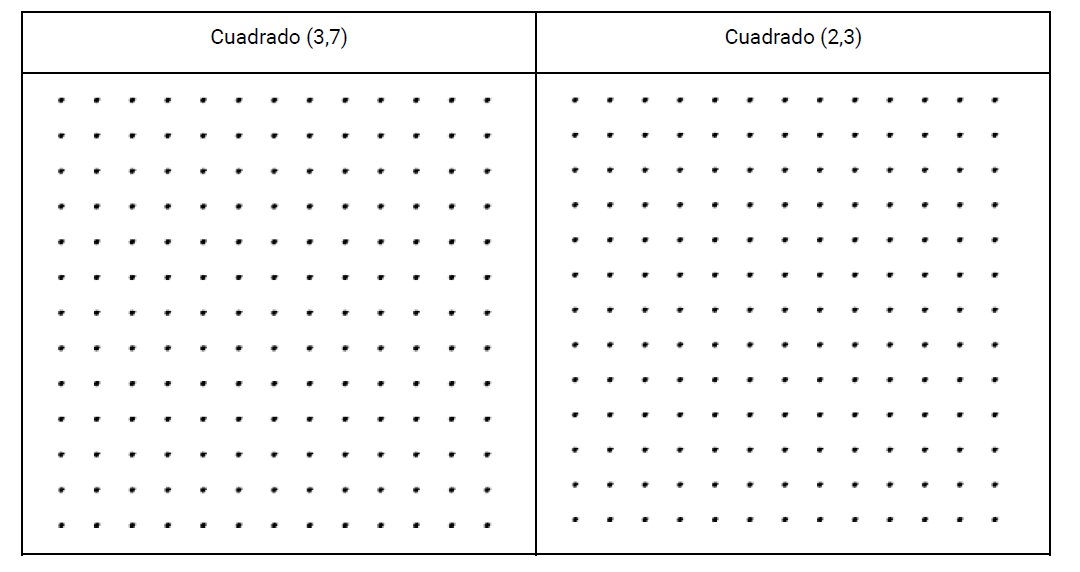
Paso necesario, porque hubo alguna dificultad para dibujarlos. Por esto no me gustan los cuadernos especialmente pulcros, sin registro de lo que ha podido pasar.

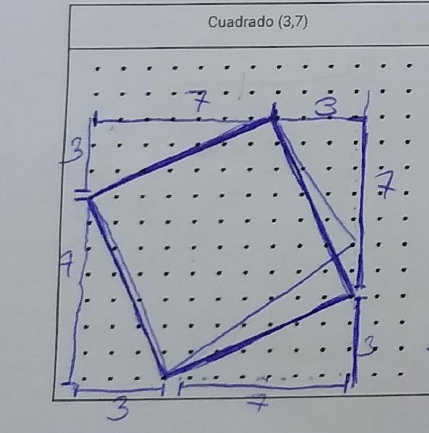
Siguiente tarea. Nos dejamos de geoplano y empezamos el camino hacia la generalización. Conexiones, esta vez, con álgebra. Se trata de dibujar a mano alzada un cuadrado $(3,b)$ y calcular su área.

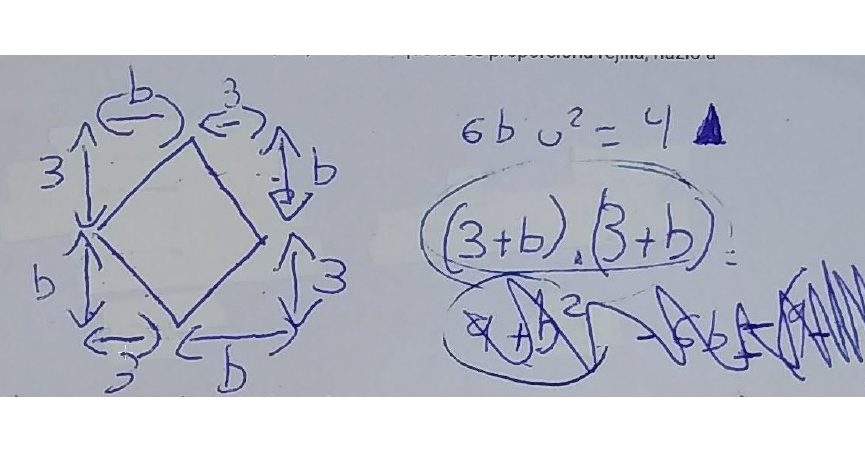
Aquí hay dos grandes dificultades. Por un lado, dibujar el cuadrado $(3,b)$ «general». Y, por otro, calcular su área, para la que les hacía falta la del cuadrado inscrito, que algebraicamente es $(b+3)^2$ y ya sabemos lo que supone. Hicimos ambas cosas meses antes, en álgebra. Por eso, esta tarea tiene especial valor. No pasa nada, nos detenemos, abordamos la cuestión y seguimos.

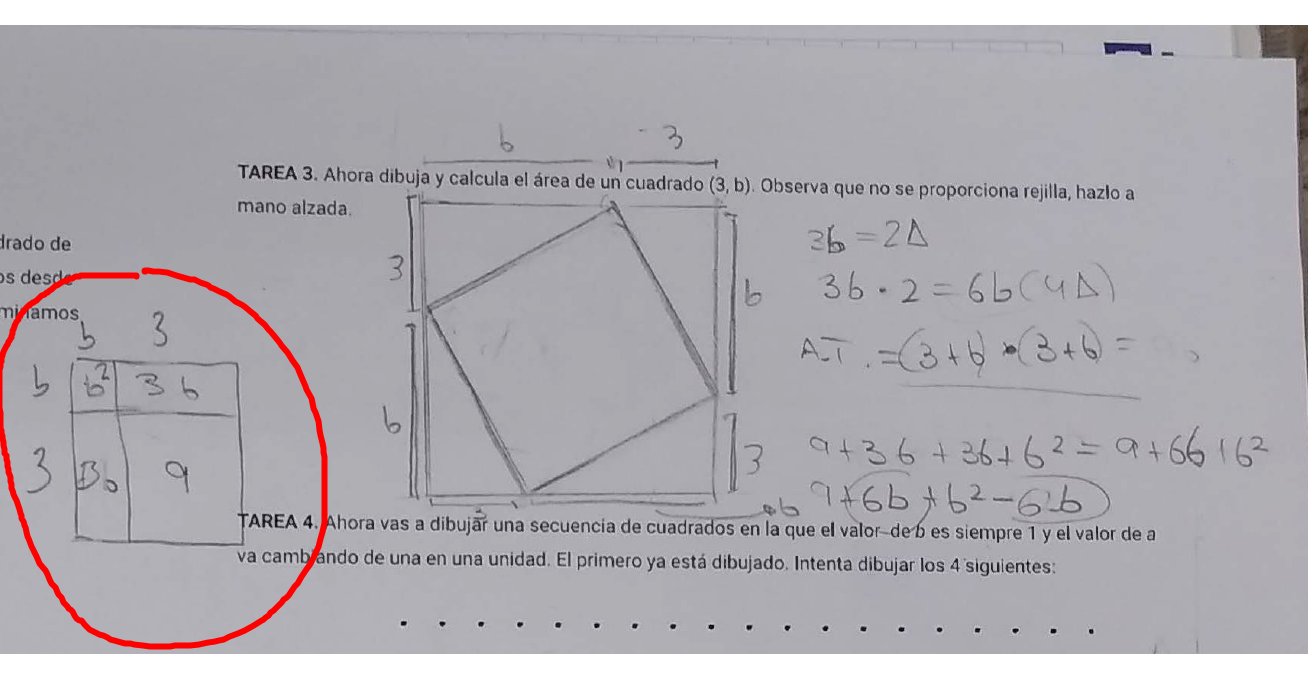
Siguiente tarea. Ahora vas a dibujar una secuencia de cuadrados $(a,b)$ en la que el valor de $b$ es siempre 1 y el valor de $a$ va cambiando de una en una unidad. El primero ya está dibujado. Intenta dibujar los 4 siguientes.

Cuestiones que tienen que responder y que luego discutimos.

a) ¿Puedes encontrar el área de cada uno?

b) Puedes encontrar un método para encontrar el área de cualquiera?

c) Calcula el área de los primeros 6 cuadrados obtenidos con el mismo método.

d) ¿Qué observas en esta serie de números que representan las áreas de estos cuadrados?

Estas preguntas son exploratorias. Básicamente, es dejarlos hacer y comparar entre ellos lo que van obteniendo. De hecho, ya hay alguno que se pispa del atajo para calcular las áreas.

La siguiente tarea estructura un poco más estas reflexiones y sugiere recopilar las áreas calculadas en una tabla como esta.

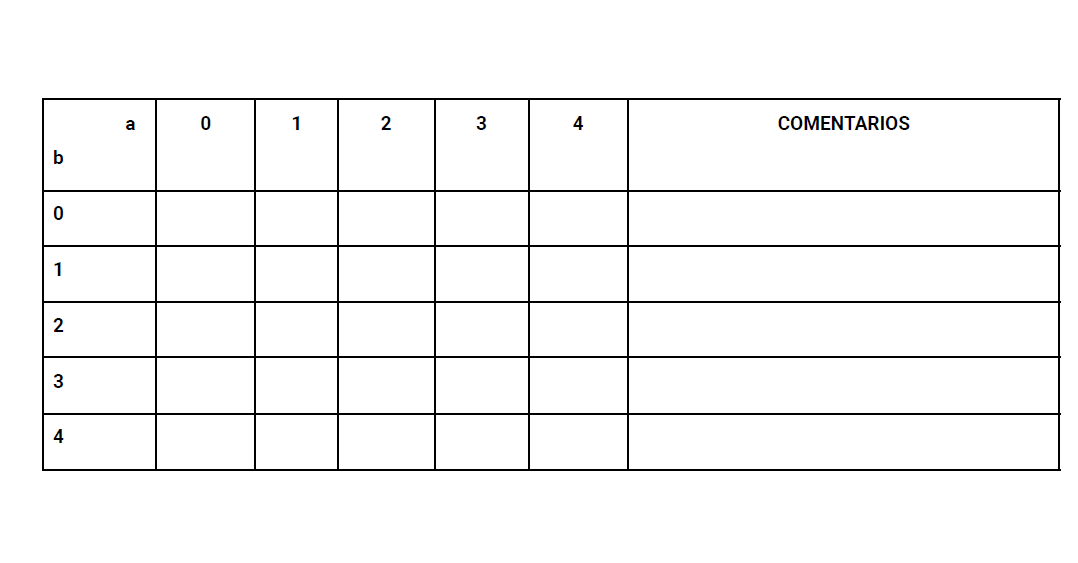
Estos están dibujados al revés, pero da un poco igual. Se comenta que es cuestión de la notación.

• Es lo mismo, ¿no? Las áreas son iguales, solo tendría que girar la hoja…

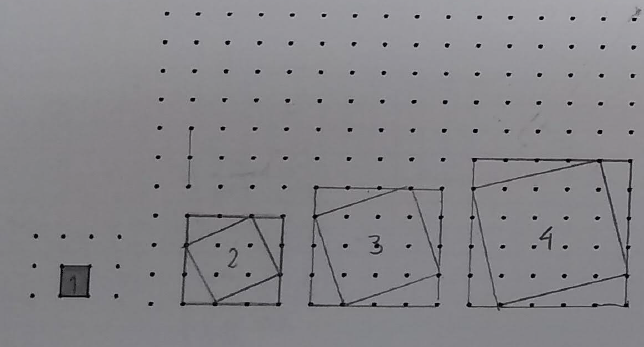
Aquí la tabla a medio hacer. ¿Se intuye lo que está pasando? Los alumnos añadían sus comentarios a la derecha:

• La fila esta es como la anterior sumando 4.
• Aquí se está sumando $b^2$.

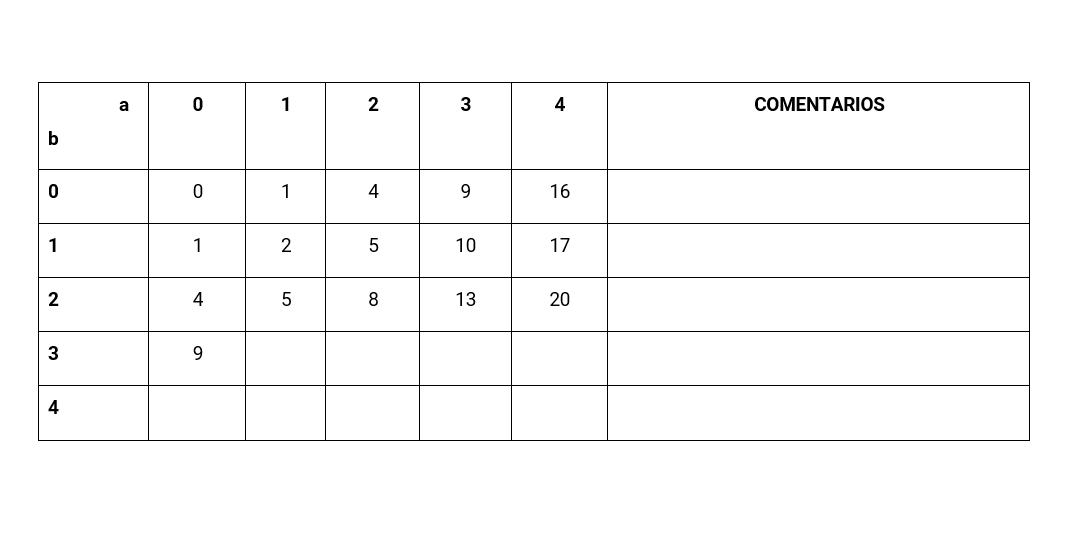
Preguntas que acompañan a la tabla y que luego se ponen en común:

a) ¿Puedes construir la siguiente fila (la que tiene para la $b$ el valor 5)?

b) ¿Y la fila correspondiente a $b$ con valor 10?

c) ¿Y ahora puedes escribir cuál será el área para un cuadrado $(a,b)$?

Observad que las respuestas aquí ya juegan mucho con la simbolización. Estamos formalizando ya la idea central del teorema de Pitágoras. Por lo menos, hemos resuelto el problema de inicio. Calcular el área de esos cuadrados inclinados.

Porque mira que es petardo el profesor de Matemáticas. No, nos puede dar el lado y ya. Nos pone el cuadrado inclinado. ¡Qué necesidad!

• Es que si os doy el lado es una tontada de actividad…

Por si no ha quedado claro el asunto, se propone dibujar un cuadrado general $(a,b)$ y obtener el área.

El colofón

Vamos cerrando la construcción. Compara las áreas de la parte sombreada y explica tu método.

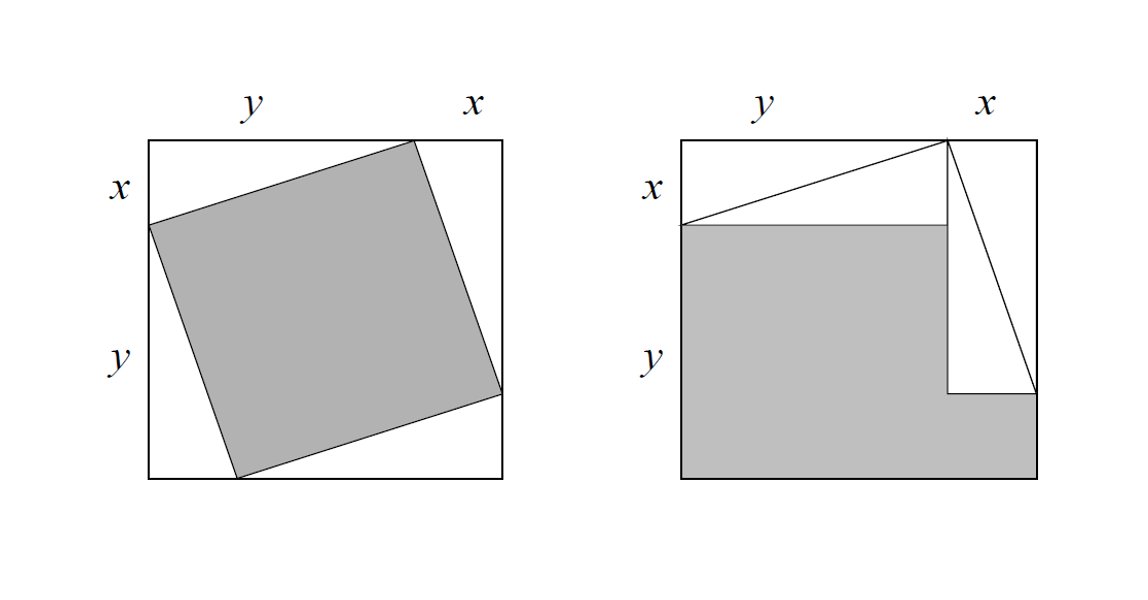
Preguntas. Empezamos suave:

a) Si las dos áreas analizadas arriba son iguales, entonces escribe las conclusiones que se pueden observar.

Y… la pregunta:

b) Si ahora pensamos en que el lado del cuadrado gris de la izquierda mide c, indica cuánto es el área de ese cuadrado y escribe de nuevo las conclusiones del apartado anterior.

Ahora sí. Pues había un matemático que se llamaba Pitágoras que, en torno al siglo VI a.C., le daba vueltas a estas cosas…

Las tareas realizadas hasta aquí son básicamente las que se proponen en la unidad «Discovering the Pythagorean Theorem» del Mathematics Assessment Project. Ya sabéis lo fan que soy del Shell.

¿Cómo continuamos?

Pues poniendo sobre la mesa diferentes pruebas de Pitágoras. La idea sale de otra fuente imprescindible de recursos: NRICH.

Se trata de proponer diferentes pruebas de Pitágoras y trabajarlas. Tampoco es necesario que todos los alumnos hagan todas. Aquí entré a clase con la idea de repartir por secciones de aula según mi criterio, pero como se pusieron al tajo por la que les dio la gana, me amoldé.

La presentación de la actividad. Ahora ya sabes que el teorema célebre se llama Teorema de Pitágoras. ¿Qué significa? Te vamos a proponer varias pruebas. ¿Cuál te parece más convincente? ¿Cuál te resulta más fácil de entender? ¿Cuál te resultaría más fácil de explicar?

Primera prueba. Los recortes. ¿Siempre podemos hacer esta descomposición?

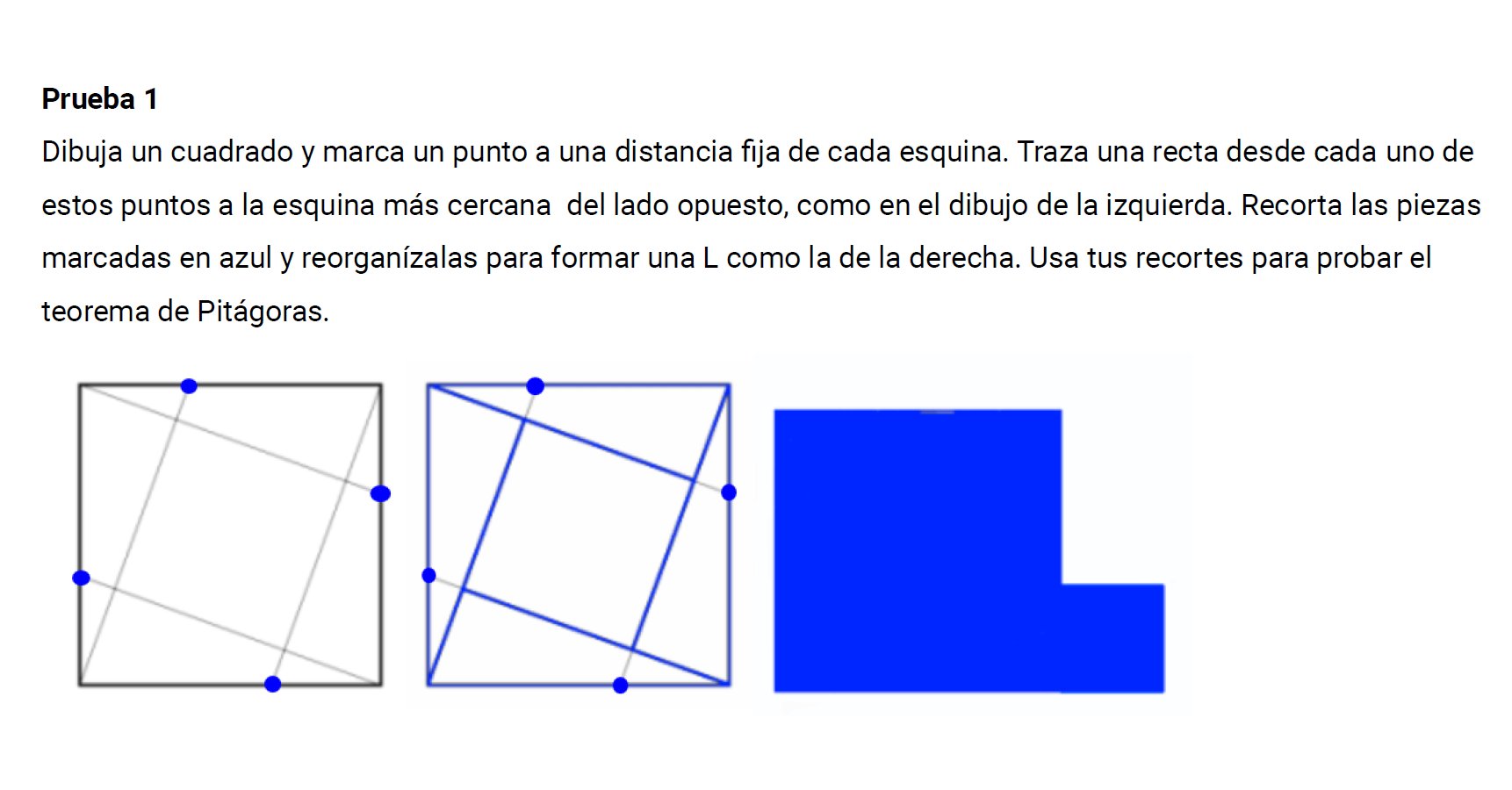
Segunda prueba. En el link de nrich que he puesto antes hay un applet bastante majo de Geogebra. Lo usamos en clase, pero en la hoja les pusimos lo siguiente.

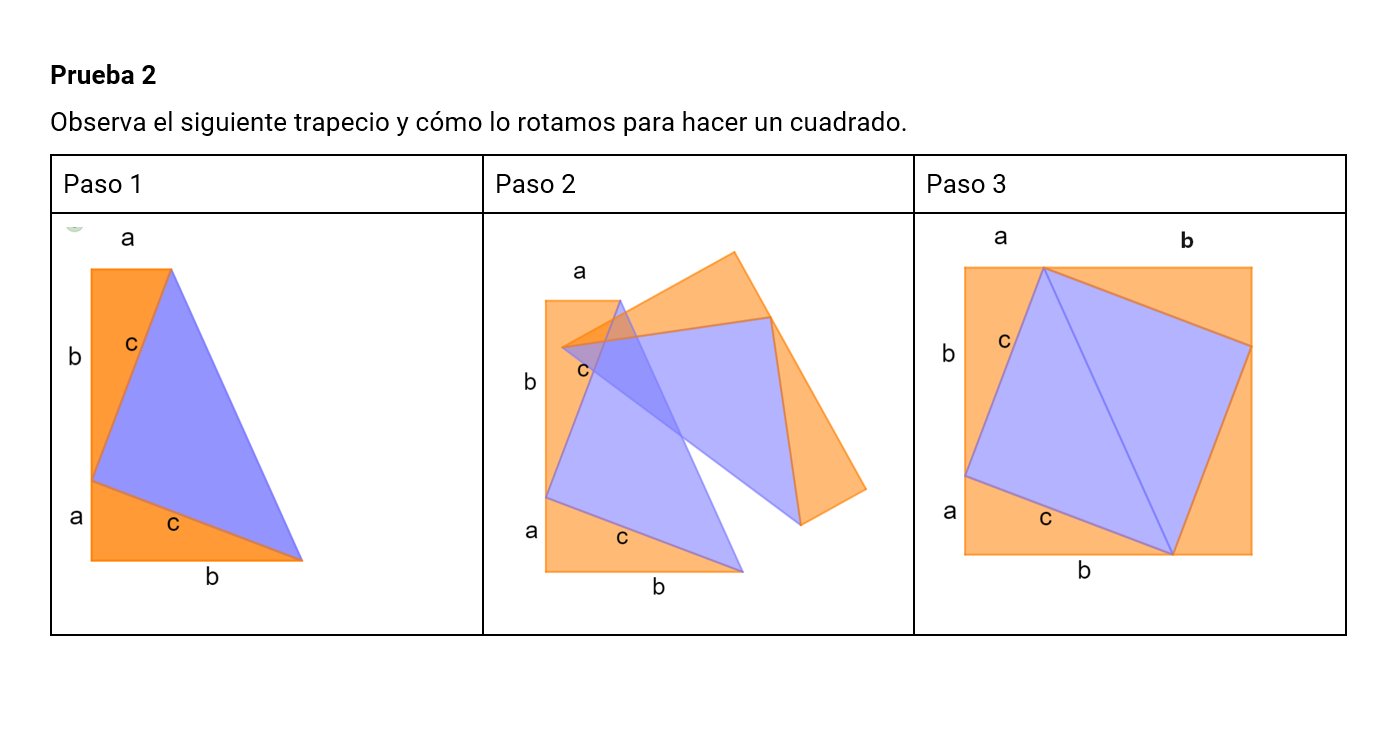
Con un poquito de andamiaje…

a) Escribe la expresión del área del cuadrado grande del paso 3.

b) Utiliza la expresión de a) para calcular el área del trapecio del paso 1.

c) Averigua el área del trapecio del paso 1 sumando las áreas de los tres triángulos rectángulos del paso 1.

d) Utiliza los resultados de los apartados a, b y c para dar una prueba del teorema de Pitágoras explicando cada uno de los pasos.

Tercera prueba. Conexiones con proporcionalidad y asomándonos a la semejanza…

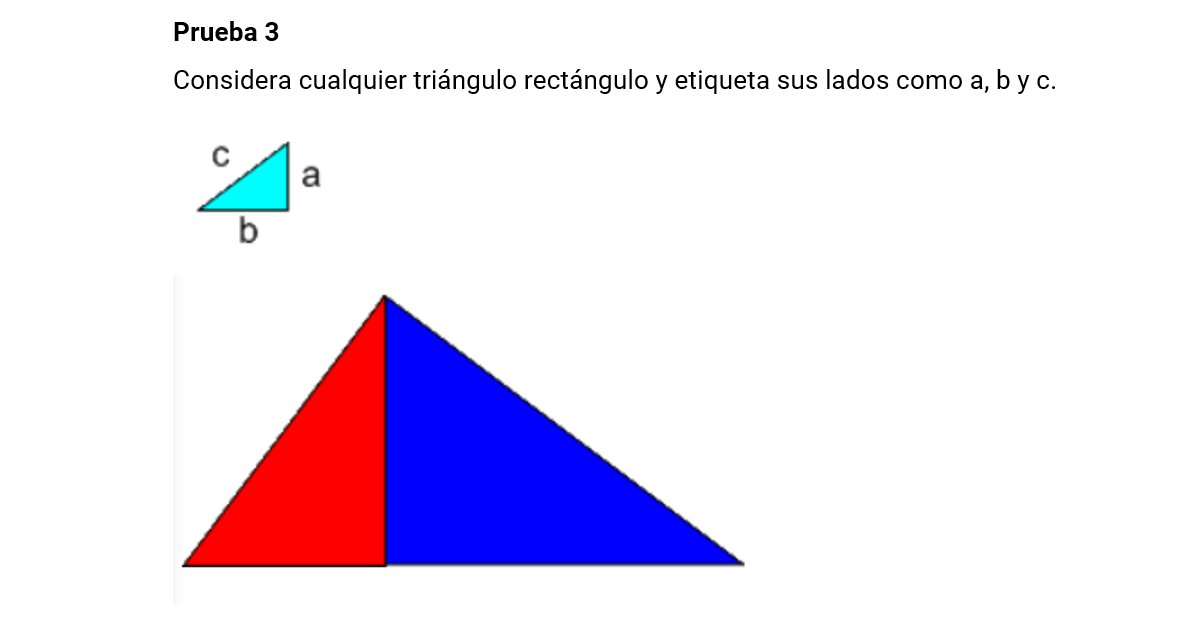
Aumenta el triangulito pequeño por un factor de escala a para hacer el triángulo rojo y por un factor de escala b para hacer el triángulo azul. Une ambos como se indica en la figura.

a) Demuestra que los podemos unir de esa manera y que ese triángulo es igual al original aumentado en un factor de escala c.

b) Utiliza lo observado en el apartado anterior para probar el teorema de Pitágoras.

Como última prueba, la «clásica» disposición. Que, realmente, ya estaba trabajada.

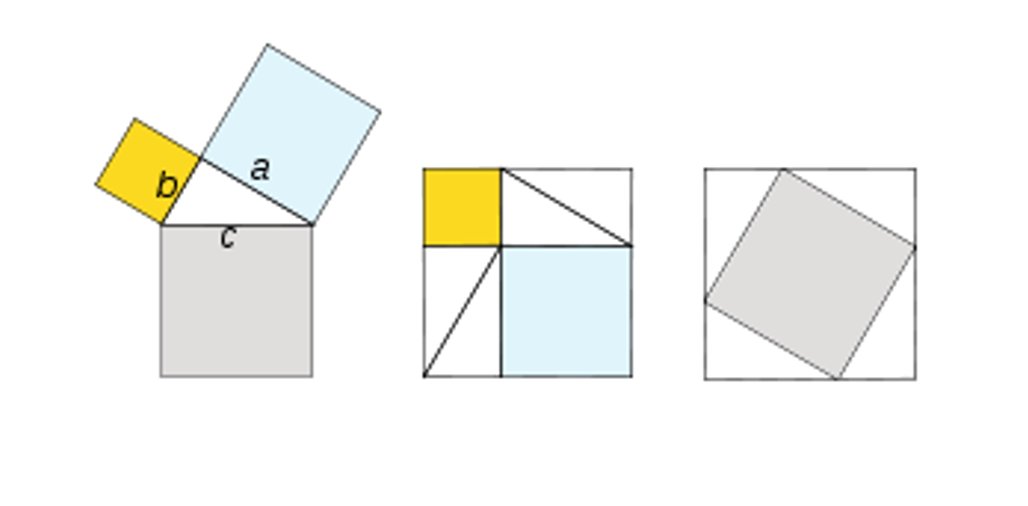
Problemas de aplicación

Finalmente, problemas de aplicación. Alguno que otro sacado de nrich y alguno que otro inventado (cálculo de distancias del fusor de una impresora 3D…).

Sí que hay tres de nrich que quiero dejaros por aquí.

Uno que parece una tontería, pero que tiene más jugo del que parece: Si dos de los lados de un triángulo rectángulo miden 5 cm y 6 cm, ¿cuántas posibilidades hay para la longitud del tercer lado?

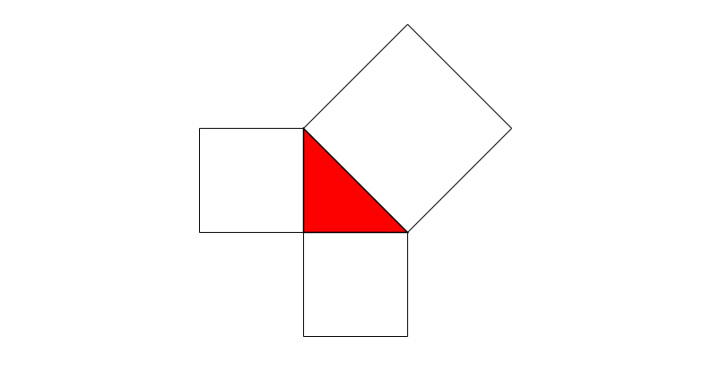
Otro que admite varias aproximaciones: El triángulo de la figura es isósceles. Se ha dibujado un cuadrado sobre cada uno de sus lados. La suma de las áreas de estos tres cuadrados es 72 cm2. ¿Cuál es el área del triángulo?

Y otro, también recogido en nrich, pero que llega desde el fantástico blog de Don Steward (DEP). Que, por cierto, no es nada inocente de entrada.

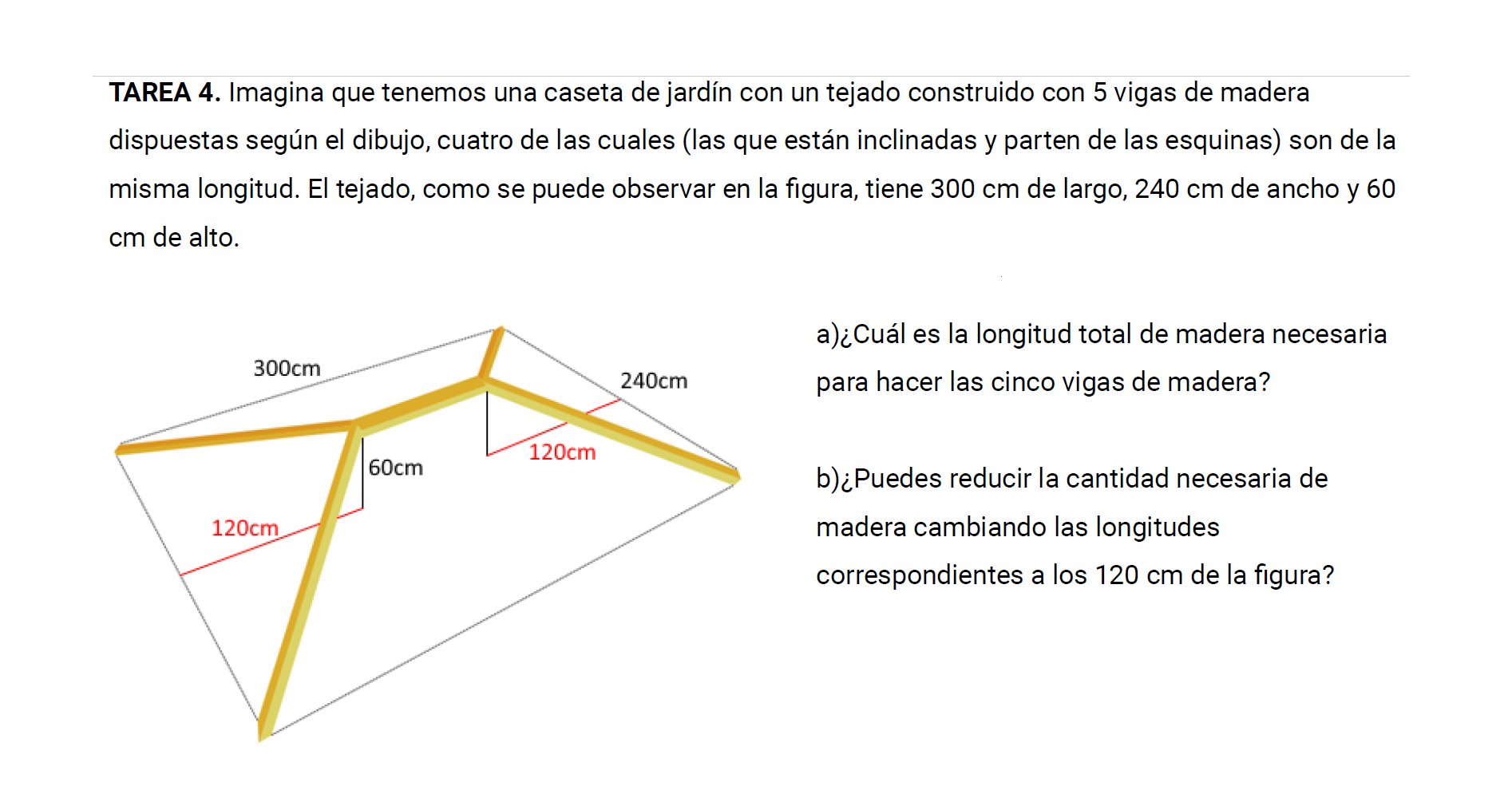
Ojo con este último porque es un ejemplo magnífico de techo alto. ¿Y si utilizamos variables? ¿Sabrías obtener la expresión algebraica? Puede que sea uno de los primeros problemas de optimización a los que se enfrenten.

La secuencia está abierta a mejoras o a incluir otras tareas, claro. Por ejemplo, se queda en el tintero el interesante camino que se abre al generalizar el teorema construyendo sobre los lados del triángulo rectángulo otras figuras que no sean cuadrados.

Confío en que hayáis disfrutado con el hilo. Para afinar la propuesta fueron indispensables las sesiones de trabajo con mi compañera de no-departamento Ana Martínez. (Esto de las no-cosas son cosas de los CPI de aquí).

Porque no se trata solo de plantear las tareas. Eso solo es el primer paso. Se trata de explotar las discusiones al máximo. Y, para ello, las conversaciones sobre cómo están yendo estas secuencias en clase son de lo mejor.

Pd1. Este es otro de los de «Elige tu propia aventura» porque, para los que me seguís hace poco, planteé el de la mediatriz de la misma manera. En cualquier caso, hay más hilos similares por mi perfil y, al poco, los dejo en mi blog.

Pd2. Es posible que más adelante os hable de la evaluación de esta secuencia. Como todo lo de este curso, basada en autoevaluaciones sistemáticas y en la mejora continua.

Material relacionado

La fundamentación de la secuencia está desarrollada en este artículo

Los materiales los dejo aquí por si vienen bien.