Sobre una secuencia de enseñanza de la medida de infantil a secundaria
Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.
Actividad en 2º ESO: mide el área del mantel (amarillo) tomando como unidad la servilleta (naranja). No te creerás lo que pasó a continuación.
Hilo sobre medida en el Día Internacional de las Matemáticas #idm314
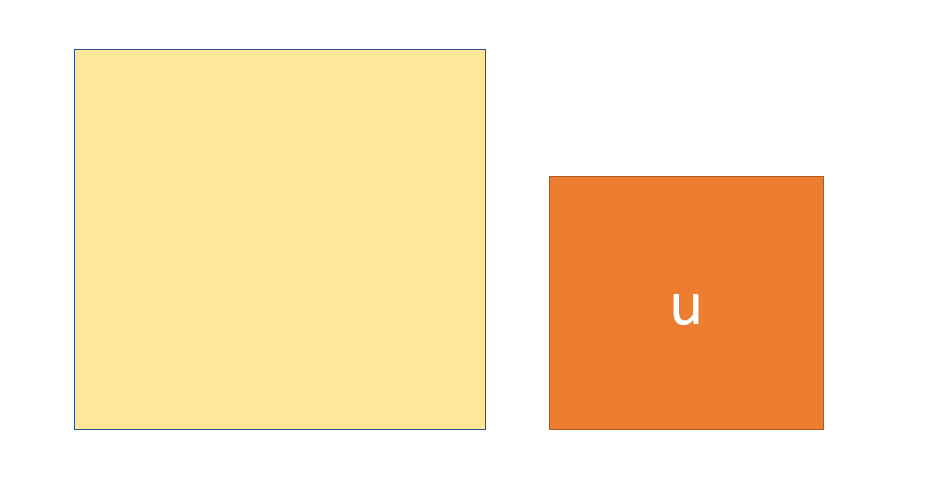
Efectivamente, hay alumnos que sacan una regla, miden el largo y ancho del mantel, multiplican y te dicen que el área mide no sé cuántos centímetros cuadrados.
- No, tomando esto (la servilleta) como unidad.
- ¿Ein? [Insert aquí cara de «pero qué me estás contando»]
También los hay que miden el perímetro con la regla y te dicen que el área mide tantos centímetros. Ojo, que estamos hablando de alumnado de 13-14 años de edad.
Que a lo mejor nos ponemos a hablar alegremente de unidades, fracciones y demás cosas del montón y a saber lo que estará pasando por esas cabecitas.
Eso sí, la escalera para cambiar unidades se la conocen todos. Porque parece que hablar de medida en primaria es hablar de cambios de unidades del sistema métrico decimal (con la escalera o regla similar). Eso, y aprender sobre el sistema monetario.
Resulta que aprender sobre el sistema monetario es… aprender sobre el sistema monetario. Sí, vale, hay una magnitud, que es valor económico. Y este valor puede expresarse con diferentes unidades, como euros o dólares. Sin embargo, ¿qué procesos de medida ponemos en juego?
Es decir, ¿cómo puedo adjudicar un valor económico a determinado objeto? ¿Cómo se establecen las equivalencias entre las diferentes unidades? Aunque estos procesos existen con esa magnitud, quedan muy, muy lejos de lo que debería ser la medida en infantil, primaria y secundaria.
Me habéis leído poner a caldo la dichosa escalerita para el cambio de unidades. Este es el hilo que (quizás) estabais esperando y que intenta sintetizar de qué hablamos cuando hablamos de MEDIDA.
Las investigaciones de Piaget dieron lugar al establecimiento de estadios evolutivos en esto de la medida:
- Comparación perceptiva directa.
- Comparación por desplazamiento de objetos.
- Medida con unidades objetales.
- Medida con unidades convencionales.
Ello propició el diseño de secuencias didácticas en las que, por ejemplo, no se abordaban tareas de medida de cierta magnitud hasta que el niño o la niña fueran conservadores. Sin embargo, Carpenter y otros investigadores mostraron que la cuestión no era tan dicotómica.
Mostraron que plantear tareas de medida podía favorecer el desarrollo de la idea de conservación. Después expondremos los diferentes tipos de situaciones de enseñanza, pero primero vamos a detenernos en la ya mencionada noción de conservación y en la de transitividad.
¿Qué es conservar? Decimos que un niño o una niña son conservadores respecto a una magnitud cuando son conscientes de que, aunque cambie la forma, posición u otras características del objeto, hay algo que permanece constante, que se conserva.
Toma esta pastilla de plastilina. Toma esta otra, mira, antes de darte esta, voy a hacer una bola con ella. ¿Cuál pesa más? Lo que se conserva ahí es la masa. Hemos cambiado la forma, pero la masa permanece constante.
Otro ejemplo con la magnitud longitud consiste en presentarle dos juguetes a un niño o una niña, poner en medio una pared de bloques de construcción y preguntar: ¿están ahora más cerca los juguetes? ¿más lejos?
¿Qué es la idea de transitividad? Posiblemente te suene haberla visto en lenguaje formal. Si a≥b y b≥c, entonces a≥c. Pues aquí es lo mismo, pero expresado en cantidades de magnitud.
Es decir, si un objeto A presenta una cantidad de magnitud igual a la de un objeto B, y la cantidad de magnitud de B es igual a la que presenta un objeto C, entonces A y C tienen la misma cantidad de magnitud. Esto se extiende si cambiamos los iguales por desigualdades.
Vamos con las situaciones de enseñanza que conformarían un trabajo en medida desde infantil hasta secundaria. Los numeritos indican cierta progresión, pero esta progresión habría que verla para cada magnitud.
En todo caso, no es una secuencia fija. Y nos podemos imaginar situaciones de enseñanza que combinan algunas de estas que nombraré, que podríamos llamar «fundamentales».
1. Situaciones de identificación y conservación de la magnitud
Como ejemplos, ya he comentado lo de la plastilina y lo de la distancia con una pared. ¿Alguien está pensando que esto es algo propio de infantil?
Estas figuras… ¿tienen la misma área? ¿el mismo perímetro? La confusión área-perímetro es algo que pervive muchísimo más allá de los primeros cursos de primaria. Si cambia el perímetro… ¿cambia también el área?
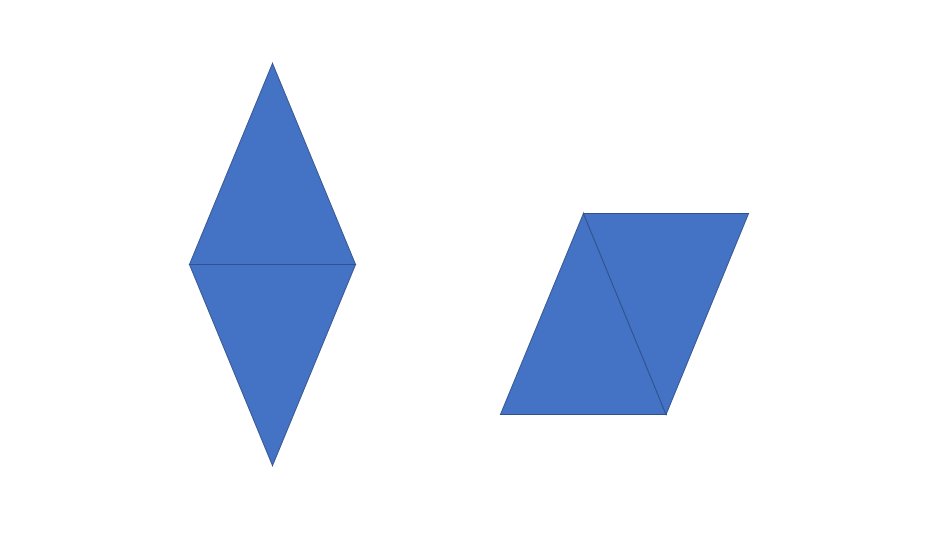
¿Alguien está pensando que esto es algo que ya tiene superado del todo como persona adulta? Os invito a pensar qué pasa en esto de aquí.
📷 Trekky0623
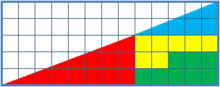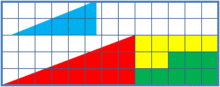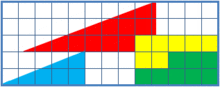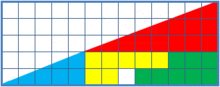
De verdad, pensadlo antes de buscarlo en internet. Os dejo las imágenes en grande para vuestra comodidad.
📷 Dnu72
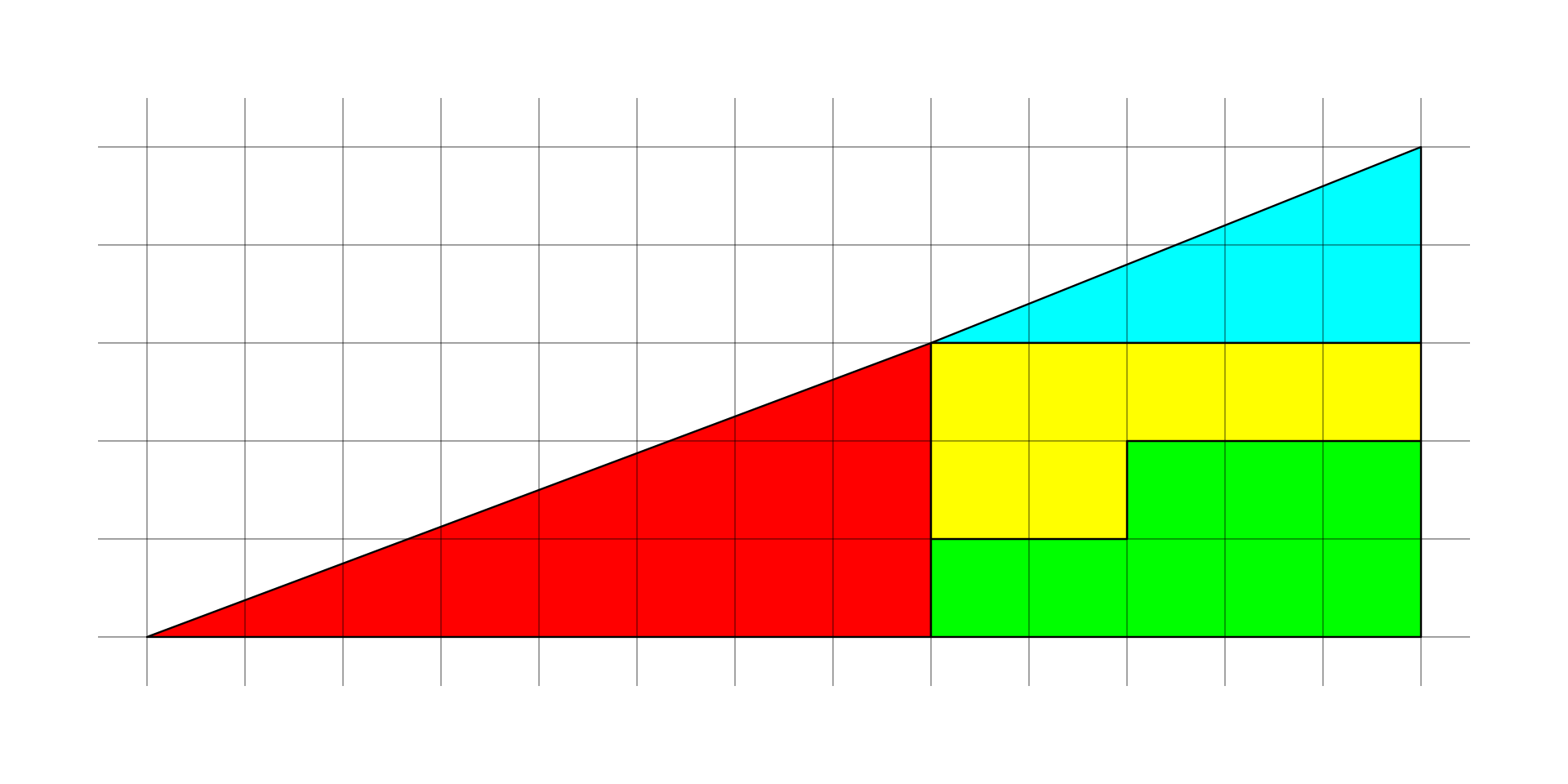
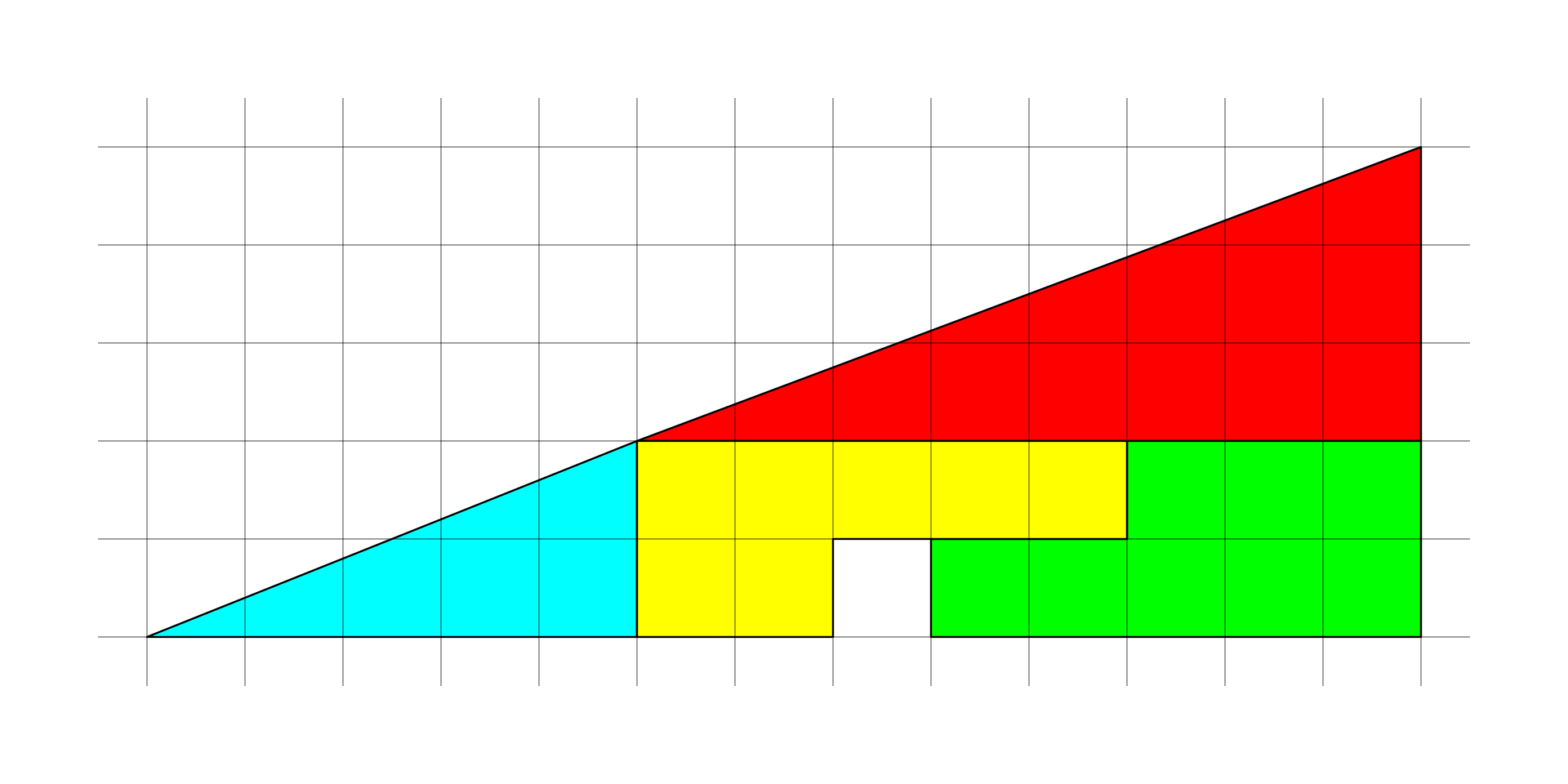
2. Situaciones de comparación directa de cantidades de magnitud sin objetos intermedios
¿Cuál de estos útiles de escritura es más largo?

Esto lo puedo resolver alineando los extremos, sin utilizar ningún objeto adicional. A veces, incluso, se puede responder a este tipo de pregunta comparando por percepción visual.

Cabe observar que todavía no hemos medido nada. Y es que, para comparar no tenemos por qué estar midiendo nada.
3. Situaciones de comparación cantidades de magnitud con objetos intermedios
Mira, tengo esta mesa y quiero saber, sin moverla, si cabrá por la puerta. En la clase podemos tener listones o tiras de papel o de tela.
Podemos coger una tira de papel y utilizarla para marcar la cantidad de longitud presente en el ancho de la mesa. Luego, con esa tira vamos a la puerta, y si la cantidad de longitud del vano es mayor a la de la tira, concluimos que la mesa cabrá.
No hemos medido nada, solo hemos aplicado la idea de transitividad. Obviamente, esto también podría haberse resuelto midiendo. Por eso, es bueno retomar este tipo de situaciones más adelante jugando con las variables didácticas, como el material a disposición del alumnado.
4. Situaciones de ordenación cantidades de magnitud
Dentro ejemplo con la magnitud capacidad. Ordena estos vasos de mayor a menor capacidad. Os invito a realizar esta actividad sin medir, solo trasvasando.

Trasvasar. Rebosar. Llenar. ¡Cada magnitud tiene su propio vocabulario asociado!
La situación de los vasos se puede hacer con un objeto intermedio, poniendo a disposición un recipiente mucho más grande sobre el que marcar la cantidad de magnitud de cada uno. O midiendo, claro, con una cazoleta o similar.
Me gusta pensar en las variables didácticas como mandos de control para sacar todo el jugo posible a una situación en diferentes momentos.

Antes de seguir, voy a dejar una pregunta, como ejercicio. Cuando comparamos el peso de dos objetos con una balanza, ¿es la balanza un objeto intermedio? Me encanta el debate en #cosicasdeDAII.
5. Situaciones de medida con unidades antropométricas o arbitrarias: de cálculo y de construcción
Empezamos con la medida. ¿Empezamos con el SMD? No. Comenzaremos con unidades objetales (tazas, listones, etc.) o antropométricas (palmos, pies, etc.). En definitiva, arbitrarias.
Distinguiremos entre situaciones de cálculo, donde nos dan un objeto y tenemos que averiguar su cantidad de magnitud; y de construcción, donde tenemos que construir cierto objeto con una cantidad de magnitud determinada.
Situaciones de cálculo son medir la capacidad de una jarra en tacitas, expresar recetas de cocina en medidas de la abuela (ojo con esto, porque ese «harina, la que coja», jejeje), medir el área de la mesa en hojas de papel, etc.
La situación del tuit original es una situación de medida de cálculo, con la magnitud área, para abordar la representación fraccionaria del número racional. Se puede hacer en 2º de ESO tranquilamente. Si se hubiese hecho en 6º EP, bastaría algo muy breve o cambiar de magnitudes.
Resulta que esta situación obliga a hacer subunidades.
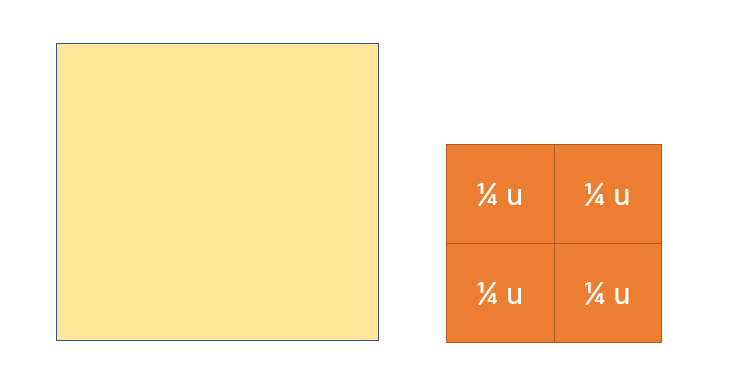
Y como necesito 9 de esas unidades, el mantel mide 9/4 u.
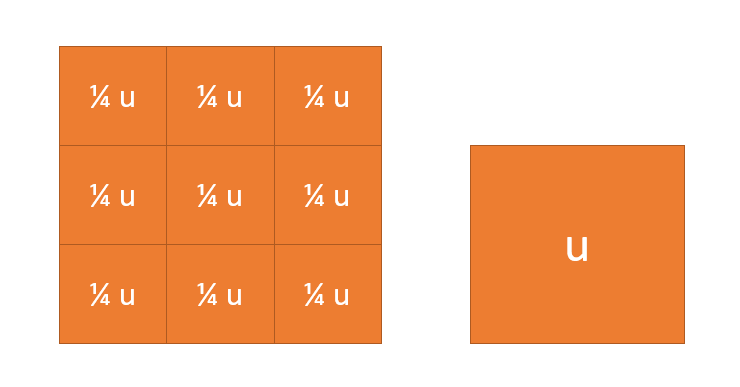
Esto es medir áreas de manera DIRECTA. Fundamental haber hecho en primaria este tipo de situaciones. Mide esta hoja con estos rectangulines. Mide esta otra. Compara. Etc.
Cuando empleamos las fórmulas de las áreas estamos midiendo áreas de manera INDIRECTA. Porque medimos longitudes y luego operamos con ellas para dar con el área. Hay magnitudes que solo podemos medir de forma indirecta, como la temperatura.
Como ejemplo de situación de construcción, podríamos plantear recortar el forro necesario para forrar un libro, sabiendo que el área es de tantas unidades.
6. Situaciones en las que resulta necesario utilizar las equivalencias de los sistemas de medida
¡Anda! ¿Cómo? Equivalencias sin haber introducido el SMD. Efectivamente. Mira, esto es del episodio de «El problema del tesoro enterrado» de Peg+Gato (serie para 5-7 años).

Mide el área de esta hoja con estos rectangulitos azules. Ahora mídela con estos rojos (tienen un área cuatro veces mayor, pero no lo decimos). ¿Qué observas?
Las situaciones 7 y 8 están muy relacionadas.
- ** Situaciones de medida con unidades del Sistema Métrico Decimal.**
- ** Situaciones para determinar el grado de precisión de la medida.**
Un clásico es medir el ancho de la clase con pies. A unos les sale un número y a otros, otro. ¿Qué hacemos? ¿Usamos el zapato de María como unidad estándar? ¿Y si queremos encargar un mural? ¿Enviamos el zapato de María con el pedido? ¿Qué hacemos? ¿Cómo solucionamos esto?
La cuestión es que los niños, actualmente, están en contacto continuo con el SMD, y la respuesta a esa pregunta es prácticamente directa. Mucho mejor medir en metros, claro. Nos hemos puesto de acuerdo en muchos países para medir las cosas.
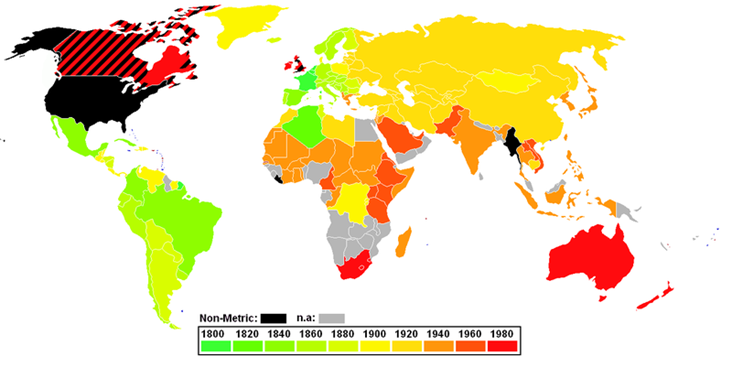
La situación 9 es transversal completamente a todas las anteriores:
9. Situaciones de estimación de la medida de cantidades de magnitud y ejercitación del cálculo mental en situaciones de medida
No es estimar «en plan adivinar», no.
Podríamos distinguir situaciones de estimación con la unidad presente o no. O situaciones de estimación por exceso y por defecto, tanto a priori (antes de echar las cuentas) como a posteriori (después de echar las cuentas).
Escribía en EDMA0-6 sobre situaciones de estimación en Cyberchase (ver este post).
Y hasta aquí el esbozo de lo que constituye el tratamiento de la medida. Importantísimo en la fundamentación de conceptos matemáticos como el racional.
Todo esto es una especie de resumen de lo que se les cuenta desde @dm_unizar en #cosicasdeDAII a los alumnos de @FacultadEducaUZ desde hace tiempo.
Os enlazo también un hilo que hice sobre el tratamiento de la medida en esa maravillosa serie que es Peg+Gato.
Nada más, feliz #PiDay (que, aunque no hayamos nombrado a Pi, también se fundamenta en todo esto de la medida). Y feliz Día Internacional de las Matemáticas #idm314.