Gafas matemáticas para ver dibujos animados: Blaze y los Monster Machines

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

Me encanta usar mis gafas #matemáticas para ver dibujos animados. A través de ellas, os voy a hablar de «Blaze y los Monster Machines». Poneos vuestro pijama favorito esta fría mañana de fin de semana, que vamos a ver la tele.

Dentro hilo

Cada episodio está enfocado a un contenido STEM diferente. Aquí me ocuparé de la M, aunque aparezca en contextos muy ligados a la S, la T y la E. Ahora está de moda añadir una A de Arts para hacer STEAM. ¡Ay! ¡Qué lío de letras!

La magnitud masa/peso, habitual en el currículo de infantil y primaria, aparece como concepto central en varios capítulos. Otras magnitudes, como la longitud, surgen de forma secundaria en muchos episodios. ¿Se abordan siempre bien?

Vamos con la masa/peso en «¡Se enciende la mecha!». Aquí han de conseguir subir a Starla con los demás. Los números en verde aparecen cuando AJ usa su casco de realidad aumentada para analizar la situación. ¿Veis algo que no encaja?

Lo primero, están compensando el peso de Starla, que es un MONSTER TRUCK, con un sofá, una lata de judías y un libro. Shh, Pablo, ¿no te has dado cuenta de que son unos dibujos sobre camionetas que hablan? ¿No estarás sacando las cosas un poco de quicio?

Bueno, no soy yo el que dice que esto es una serie diseñada y producida para aprender contenidos STEM a la vez que se entretienen los críos.

Lo segundo, ¿qué son ese 4 y ese 12? Números, vale. Pero ni se indican las unidades de medida ni tiene sentido el que sean, digamos, toneladas. Podrían ser miles de libras, o cuartos estadounidenses, aunque sigue sin estar claro.

Da la impresión de que los papás ya pueden estar tranquilos si salen números por pantalla, porque su retoño está aprendiendo. Y luego que te dicen que hay 100 granos de arroz en un vasito donde hay más de 2000 ( ver este otro hilo).

Seamos honestos. Otras veces, aunque el casco de AJ no indique las unidades (¿estará en garantía este casco?), sí que las expresan verbalmente. En este ejemplo de «Zegg y el huevo» se habla de metros.

En «Hay problemas en el túnel de lavado», el concepto central es el de ángulo, todo un clásico en el currículo desde la más temprana primaria. Parece algo fácil, ¿quién no distingue entre agudos, llanos y obtusos? Sin embargo, se trata de una noción con múltiples significados.

Giro, pareja de semirrectas, región del plano. Todo esto esconde una complejidad que origina dificultades. Volvamos ahora con nuestros amigos, que tienen que encontrar unas piezas dispersas por la ciudad.

En su búsqueda, Blaze y AJ circulan por un túnel en el que hay unas máquinas prensadoras que pueden aplastarles si pasan cuando no deben. Es lo que tienen las máquinas prensadoras, no te metas dentro de una.

AJ, preocupado por su integridad física, nos explica: “Cuando las líneas están separadas y hay mucho espacio entre ellas, forman un ángulo grande. Pero cuando están más juntas, el ángulo es pequeño, y es cuando aplastan las cosas.”

Bien, ángulos grandes y pequeños. No hay mucho que objetar salvo, quizás, un excesivo estereotipado, con todos los ángulos con una de sus semirrectas paralela al suelo. No obstante, la situación es así. Seguimos, porque los enjabonadores que persiguen se han vuelto muy locos.

Han dejado las calles llenas de espuma resbaladiza. En este punto, Blaze se va a transformar en un auto de choque, porque él lo vale (es el único transformer de la serie, envidia que le tendrán los otros). Va a ir rebotando, eligiendo la trayectoria adecuada.

Y ahora el que se pone un casco de realidad aumentada soy yo. Captura de pantalla y al @geogebra, que vamos a medir. Esta de aquí, más o menos bien, puesto que se cumple aproximadamente la 2ª ley de la reflexión (el ángulo del rayo incidente es igual al del reflejado).

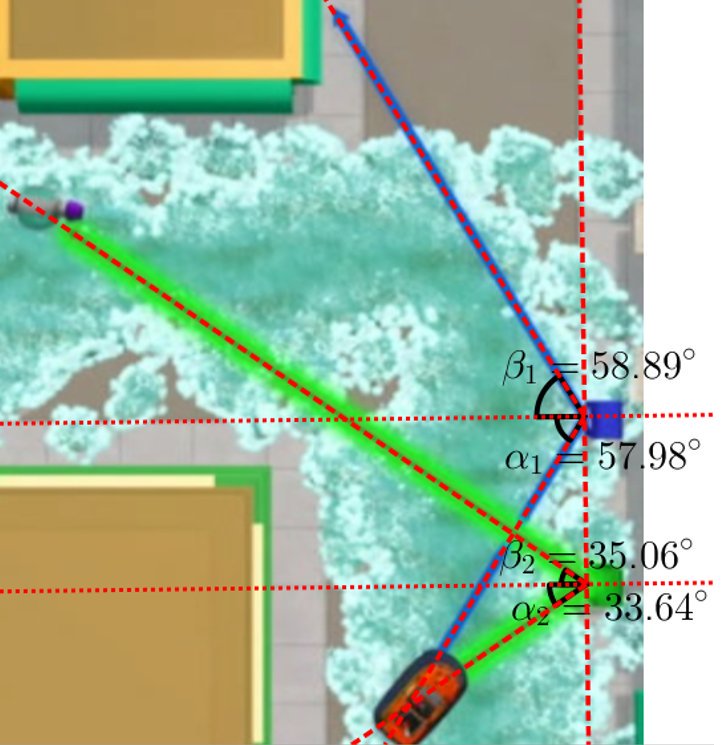
Eso sí, esta otra no hay por dónde cogerla. Una diferencia de 10º es apreciable a simple vista. Habría que tener más cuidado, porque puede conducir a la formación de intuiciones erróneas.

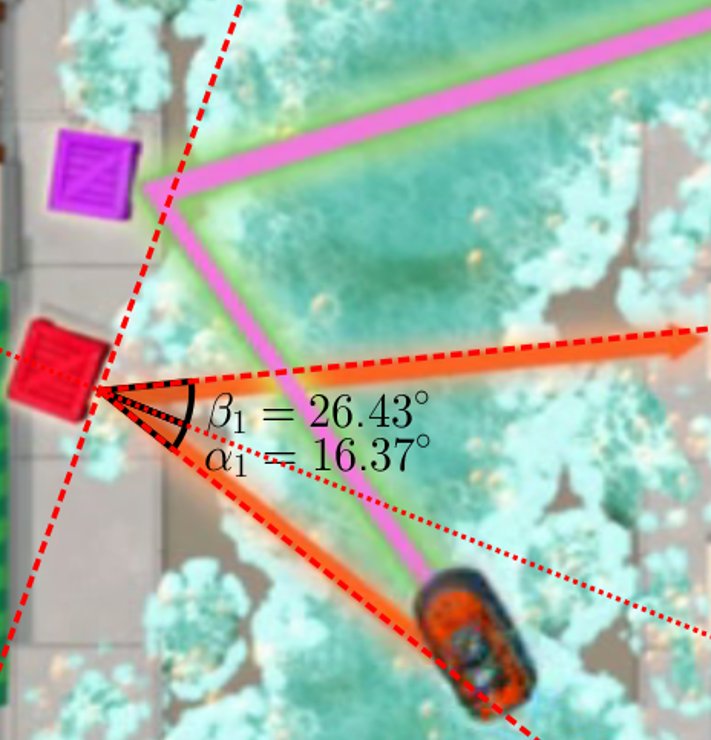
Llegamos al que para mí es el gazapo más gordo. A continuación, van a usar una rampa para aprovechar el impulso y llegar a lo alto de una torre, donde hay otras piezas.

Aquí tendremos ángulos de 5, 10, 15 y 20. ¿Grados? De nuevo el problema de las unidades, pero aquí hay algo más. Nos ponemos nuestras maravillosas gafas y… OMG.

Asumamos que ese «5» es una unidad rara, sean grados-blaze (gb). Un ángulo de «10 gb» es el DOBLE que uno de «5 gb». Pues resulta que el de «5 gb» mide unos 16º, pero el de «10 gb» mide unos 20º, que NO ES EL DOBLE de 16º. Y esto se aprecia a simple vista. Ídem para los demás.

Aquí tenemos un ángulo de 30º (perdón, grados-blaze) representado en dos situaciones distintas con ángulos que son evidentemente diferentes. Mis gafas geogebraicas lo dejan bien claro.

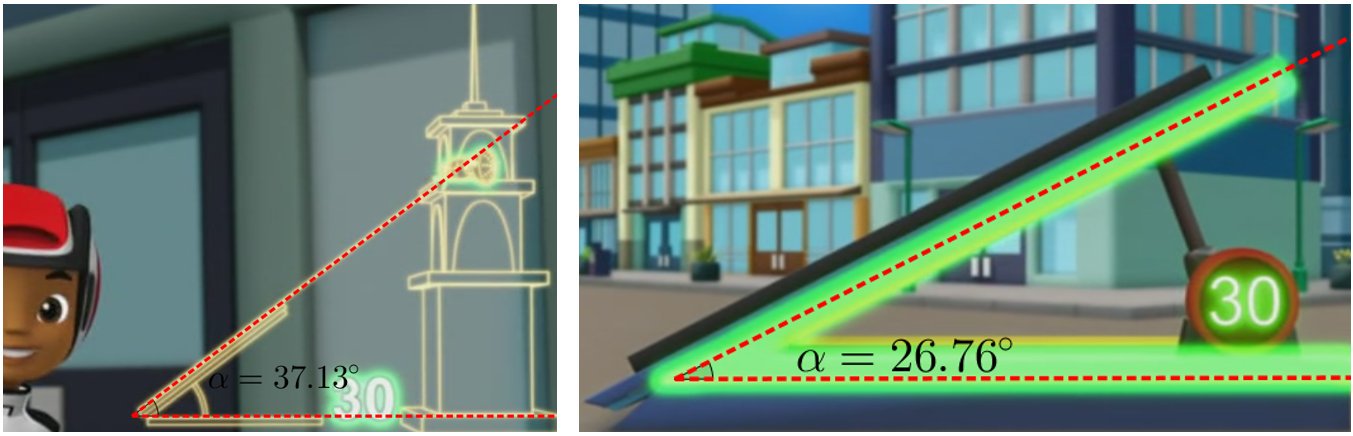
A ver si vais a pensar que soy un fundamentalista del rigor y que prohíbo ver Blaze a mis renacuajos. Pues no. Lo que sí les limitamos es el tiempo de ver la tele y hablamos un poco sobre las mates y demás elementos STEM que aparecen.

Casi acabando. A ellos les divierte esto de la caza del gazapo y así van empezando a meterse en la cabeza que no todo lo que sale por los medios es verdad. Si te ha gustado este hilo, pásate por la sección «Matemáticas animadas» de EDMA0-6. O mejor…

Ven a #Zaragoza a las III JEMA @sapmciruelos al taller que he preparado con JMª Muñoz. Bueno, o a otro, porque aquí hay competencia de la buena, y luego echamos una charrada. #felizclase