Dados griegos, sesgos de razonamiento probabilístico y actividad de modelado en 3D

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

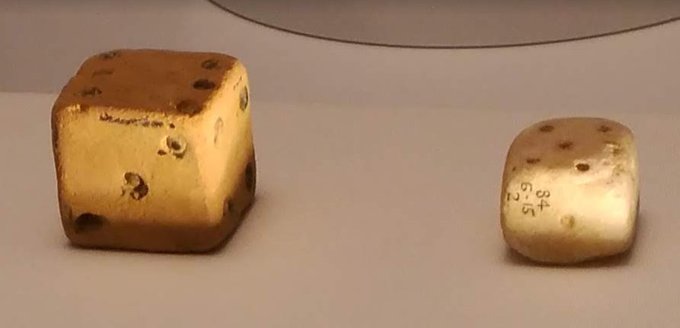
Estos dados griegos (s. V-IV aC) de la exposición del CaixaForum en Zaragoza me recuerdan mucho a los que diseñaron algunos de mis alumnos de 2ºESO de Matemáticas cuando les propuse diseñar, imprimir en 3D y probar un dado impresión3D. Dentro hilo.

La consigna de la actividad fue: diseñar un dado con ordenador. Es voluntario y añade 0,5 puntos al examen de geometría. Después, imprimiré en 3D vuestros dados, que os podréis quedar, y os pediré que los probéis para ver si están o no sesgados.

Conste que diseñar un dado no es nada fácil. No hay más que pasarse por esta discusión en thingiverse.

Una vez diseñado el dado les preguntaba

1. ¿Es este el dado que diseñaste? ¿Te gusta cómo ha quedado?
2. ¿Lo usarías para jugar a algún juego de mesa?
3. ¿Cómo sabrías si es un buen dado? ¿Hacemos la prueba?

Ningún alumno vio nada raro en su dado que le llevase a pensar que no fueran adecuados para ser utilizados en algún juego. Pero prácticamente todos tenían graves sesgos. Por ejemplo:

1. No retiraban la misma cantidad de material en todas las caras.

2. Parecido si en lugar de retirar material, se añade (lo que ya es raro de por sí)

3. No se tiene en cuenta que la suma de las puntuaciones de las caras debería sumar 7 para facilitar el equilibrado, si se hace con puntitos (tiene que ver con el error de tipo 1)

4. No se centran o alinean los puntos de cada cara, lo cual influye también en la distribución de masa del dado.

5. El dado no presenta las mismas dimensiones en todas sus caras.

El dado griego chiquitín es un claro error de tipo 5 (cogerían la piedra o el hueso que les viniera bien). Y el grandote es un intento de cubo con esquinas muy pronunciadas, que apenas rodaría. Lo otro es una canica 😊

No es fácil diseñar un dado. Los sesgos vistos con el alumnado de 2º de ESO en esta experiencia son los mismos que los de los artesanos griegos de hace más de 2400 años.

No es fácil tampoco el aprendizaje de la #probabilidad. Hay multitud de investigaciones que muestran los sesgos de razonamiento tanto en edad escolar como adulta. Es necesario plantear experiencias de aula y reflexionar sobre lo que está pasando.

Es una pena que muchas veces sea lo primero en caerse porque no da tiempo. Históricamente, esta rama tan “fácil” no empezó a estudiarse en condiciones hasta el siglo XVI (Cardano) y XVII (Pascal y Fermat). Vaya trío de ases.

Si has llegado hasta aquí y te interesa saber más sobre la experiencia de #impresión3D del dado, la describí en thalesepsilon

¡Saludos y feliz clase!