Reflexiones sobre el borrador veraniego del futuro currículo LOMLOE

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

Dejo aquí algunas reflexiones sobre el borrador veraniego del currículo de Matemáticas de Primaria. Se han leído muchas tontadas al politizarse en exceso el debate y el caso es que el documento está bastante bien.

Digo al politizarse en exceso porque está claro que esos borradores se filtraron para hacer juego. No obstante, es un error pensar que somos neutrales. Nunca lo somos. Y el currículo solo es UNO de los factores que condicionan nuestra práctica de aula.

Tengamos en cuenta que son unos borradores, por tanto, filtrados, y que a saber en qué estado están actualmente. De hecho, no sé ni si merece la pena escribir estas reflexiones, pero creo que puede ser constructivo. Permitidme seguir un orden no lineal y nada exhaustivo.

Quiero hacer especial énfasis en lo de constructivo. Soy consciente de lo complicado que es redactar una cosa de estas y que hay muchas sensibilidades que conjugar. Si no los tenéis, los compartió en Twitter @anaverboc4.

En primer lugar, mi postura es que está mejor que el anterior. Hay avances claros y, en lo que respecta a saberes, está más limpio. Por ejemplo, si me seguís ya sabréis que considero motivo de alegría que no aparezca la regla de tres.

Pienso que un currículo tiene que evitar ser una lista de técnicas. Por eso, no dudaría en eliminar esa coletilla de mediante la igualdad entre razones. No aporta nada y, en cambio, alguien puede pensar, producto cruzado y chispún. Cosa que es similar a la regla de tres.

Algo que puede sonar raro es un apartado de saberes básicos denominado Educación financiera, dentro del sentido numérico. No sé si lo habría llamado así, ni si hacía falta, pero no parece descabellado incluir el manejo del sistema monetario.

Además, al hacerlo de esta manera consiguen desmarcarlo de los contenidos de medida, que es donde aparecen en la mayoría de los libros de texto. Ya he comentado alguna vez que sí, que hay una magnitud en todo esto, el valor económico.

Pero el proceso de medida por el cual se adjudica una cantidad de magnitud valor económico a un objeto es muy complejo y está a años luz de primaria.

Sobre lo que es la medida, poco más voy a señalar. Estos son los saberes básicos sobre medida por ciclos, gracias a @kikeguerrerot, que los puso así de majos en tablas y los compartió por aquí. Si veis más capturas con estos colorcillos en este hilo, todo el crédito para él.

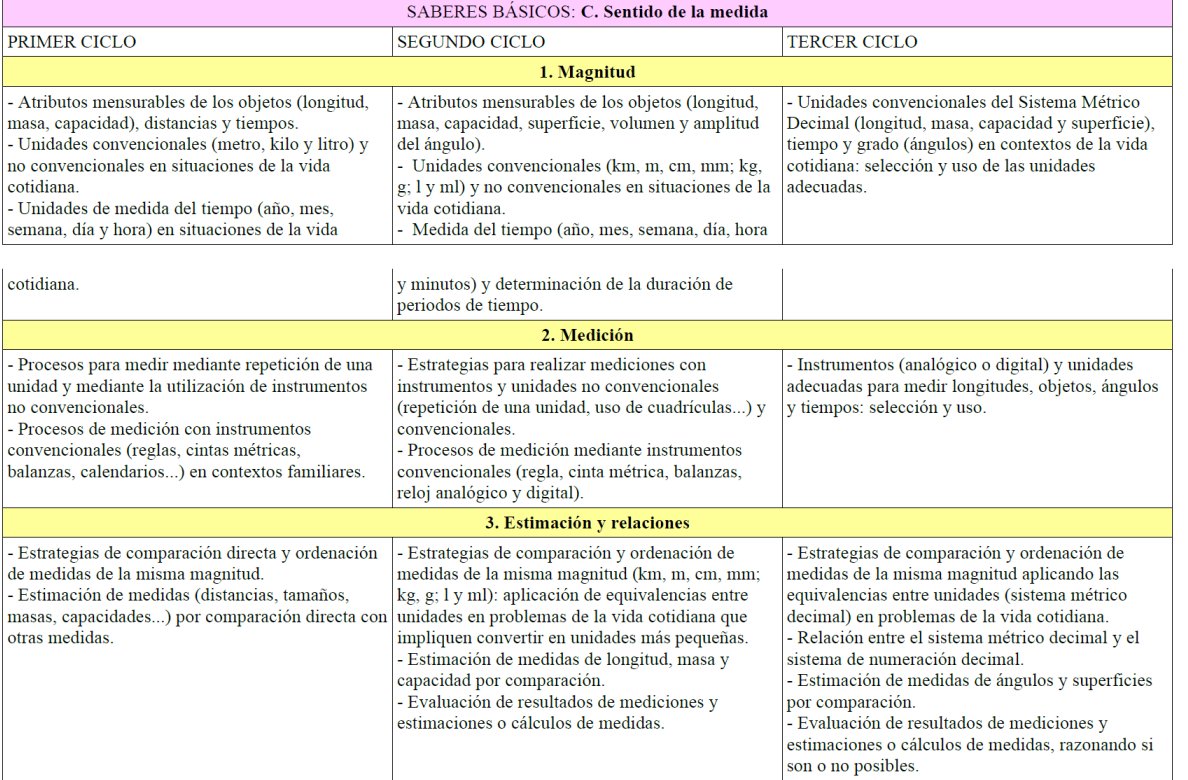
Personalmente, e hilando fino, no habría quitado las unidades no convencionales en tercer ciclo. Aunque las fracciones se introducen ya en segundo ciclo, el trabajo con unidades no convencionales puede jugar un papel estupendo en la construcción del racional.

De hecho, veo que las fracciones aparecen por primera vez como ‘Fracciones propias con denominador hasta 10 en contextos de la vida cotidiana.’ Pues bien, por qué propias. Las impropias (qué palabra más fea, pobrecitas) surgen naturalmente de las primeras situaciones de medida.

Estos comentarios van en la línea de que mi currículo ideal, si puede evitar alguna restricción innecesaria, la evita. En este caso, al indicar fracciones propias, fomentas una forma particular de introducir las fracciones: el parte-todo. Y el parte-todo tiene sus cositas.

Reconozco que con todo esto de la medida puedo tener una sensibilidad especial. Considero que su papel es transversal de verdad, no solo como contexto común a varios apartados, sino como medio para construir matemáticas de forma significativa y diferente a experimentales.

Si el tweet anterior te ha sonado muy críptico y eres nuevo o nueva por aquí, puedes leer (con calma, tiempo y ganas) el hilo² sobre medida y racional que cuelga de mi tweet fijado.

Voy saltando. En el sentido numérico creo que hay una errata al decir ‘cantidades hasta el 199’. O dices 99 o 999, pero en el momento que metes centenas, y les das significado, ¿por qué entrar con una?

No voy a debatir sobre absurdeces acerca de si las competencias no sé qué. Que se pueden definir los aprendizajes de otra manera, puede. Pero las competencias se muestran bastante operativas para distinguir lo que es el conocimiento en sí de ponerlo en juego.

Lo que sí que puedo señalar es que no le veo sentido a desgranar los criterios de evaluación de las competencias por ciclos. Observad qué ocurre con estos.

O sea, que un niño o una niña en 1ºEP debe reconocer que hay escritos unos números en la pizarra, ¿pero no interpretarlos? En todos los cursos se debería reconocer, comprender e interpretar. La diferencia está en el lenguaje y los objetos de aprendizaje.

Creo que es complicarse la vida a nivel curricular el querer detallar una competencia así. Prefiero que se describa en general y que, en todo caso, se ponga alguna actividad de ejemplo.

Porque esto pasa con casi todas. ¿En 1º/2ºEP no se puede valorar, acaso, contar hacia adelante vs usar hechos conocidos de la suma? El ciclo de modelización de problemas ha de ser completo siempre que se ponga en juego. Adaptado a cada momento, claro.

Salto a lo afectivo, que aquí han llamado socioemocional y que aparece como uno de los sentidos. Es muy necesario integrar aspectos socioafectivos en el currículo. No es una novedad, en el bloque 1 de la LOMCE se habla de emociones, superar bloqueos e inseguridades…

No sé si lo habría puesto como un sentido en sí mismo. Imagino que es una apuesta para darle valor. Desde luego, lo habría llamado socioafectivo, pues es algo más amplio que integra emociones, actitudes, creencias y valores.

Sí que lo veo como competencia, pero como saberes básicos no puedo evitar que se me haga raro. Va integrado en todo lo que se haga en clase. Además, troceado por ciclos se me vuelve a hacer más raro todavía. ¿No valoramos el error como fuente de aprendizaje en 1er y 2do ciclo?

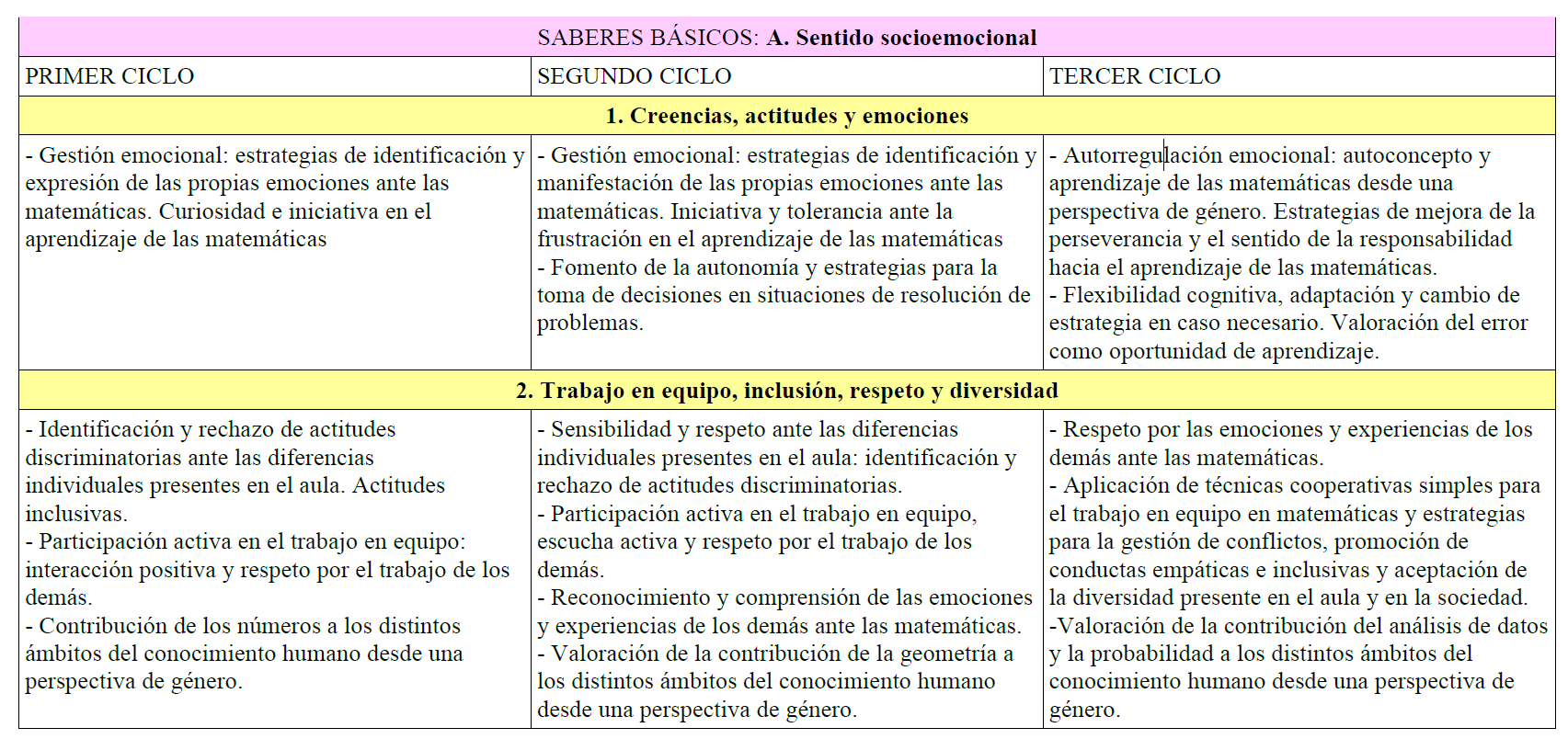
Y si echáis un ojo a la tabla de antes (como siempre, captura de las de @kikeguerrerot), veréis más ejemplos de esa complicación innecesaria. Simplemente, no veo necesario desmenuzarlo.

Creo que no procede meter descriptores de aprendizaje cooperativo dentro del currículo. Me explico. Veo que en este borrador se habla de roles, en términos que son propios de una metodología. Preferiría que simplemente se hablase de cultura de aula.

Es posible no utilizar técnicas de aprendizaje cooperativo pero, en cambio, tener una cultura de aula donde se trabaja en pequeños grupos y hay mucho intercambio. En mi caso, a mi me gusta pensar que los tengo en grupo pero no hacen ‘cooperativo’.

Al igual que no metería esto del cooperativo, tampoco veo necesario explicitar el uso de tangrams o mecanos. Son un medio. Mucho mejor si se pone un ejemplo de situación de aprendizaje como complemento. Aquí imagino que las CC.AA. podrán aportar mucho.

En lo que respecta al socioemocional y a lo afectivo, me ha parecido muy curiosa la comparación con el de Lengua. La verdad es que, después de ver el de Mates, esperaba un tratamiento de lo afectivo al mismo nivel. Y me ha sorprendido ver que para nada.

En el de Lengua -en comparación- apenas hay elementos afectivos, desde luego, no tan específicos como en Matemáticas. Por lo menos, no en los mismos términos.

Vuelvo a mates. En lo que a género se refiere, y que forma parte de ese dominio afectivo, veo especial énfasis en la necesidad de referentes. Lo cual es solo una patita de la mesa. En particular, en primaria, un referente que pueda tener el alumnado es la maestra.

Lo esencial es todo lo que tenga que ver con la cultura de aula. Esto de aquí… no tanto.

Así que yo habría tirado por aquí (captura también del borrador). No me gusta hablar de método, ya sabéis. Es una cuestión de enfoque.

Y vuelve a pasar lo mismo. Al desmenuzarlo… ¿por qué unas cosas en un ciclo y no en otro?

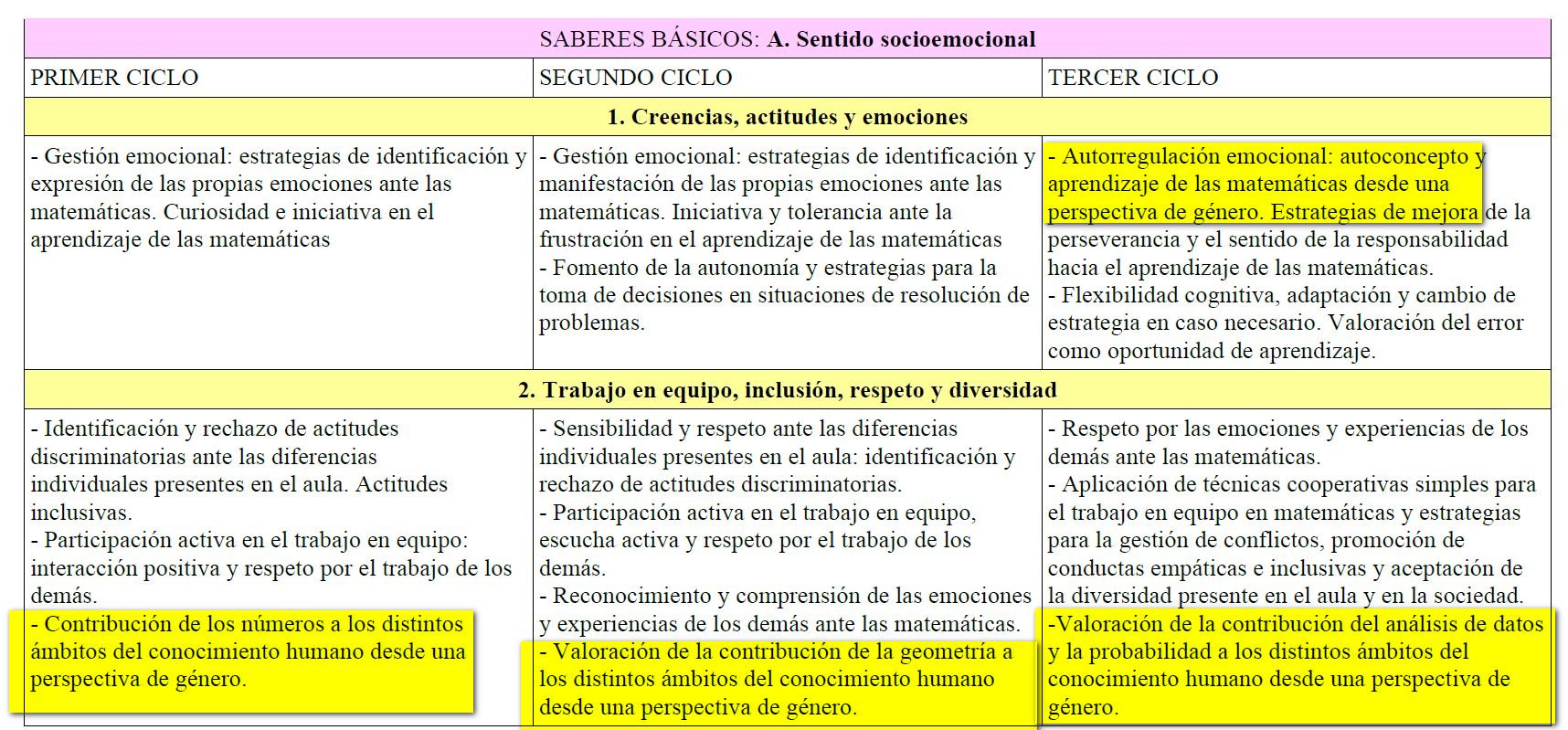
Ya voy terminando. Lo que quedaría serían más finuras. Del estilo de me habría gustado que aquí se hubiese hablado también de significados de los números, situaciones que desarrollan el significado de la suma y la resta (agregación de cantidades, comparación…), etc.

Como he dicho al principio, esto del currículo es un factor sin más de todo el conjunto. Y esto son borradores que a saber. Será interesante ver cómo quedan y cómo son los desarrollos. Ahora sí, fin.