Reflexiones ante el uso de manipulativos para el número racional (fracciones, decimales, etc.)
Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter y este otro hilo. También en BlueSky aquí y aquí
Algo característico de una didáctica específica, como la de las matemáticas, es que tiene muy presente el objeto de aprendizaje y su naturaleza. Ejemplo: si nos planteamos usar las regletas de Cuisenaire para construir el racional (fracciones…), ocurren cositas.
Hay que tener claro q son material estructurado y discreto. Y que, por lo tanto, no son lo mejor para trabajar con magnitudes continuas, como la longitud, cuya medida es lo que hace que emerja la necesidad del número racional positivo.
No es la primera vez que doy la turra con esto, ni será la última. Me fascina reflexionar sobre el uso de manipulativos. Desde luego, esto no es un alegato en contra del uso de manipulativos, ni mucho menos. Son esenciales. Pero hay que planificar su uso y ver cuál es el más adecuado. Unas simples tiras de papel aquí lo hacen estupendamente ( ver esta publicación).
¿Y con los “números decimales”?
Los bloques multibase vienen bien para cositas del sistema decimal posicional con naturales (ej., 10 u hacen 1 d). Conectan genial con técnicas intuitivas de conteo. Pero, si presento esto para q el “output” sea 3,24, ¿estaremos trabajando una representación del número racional?
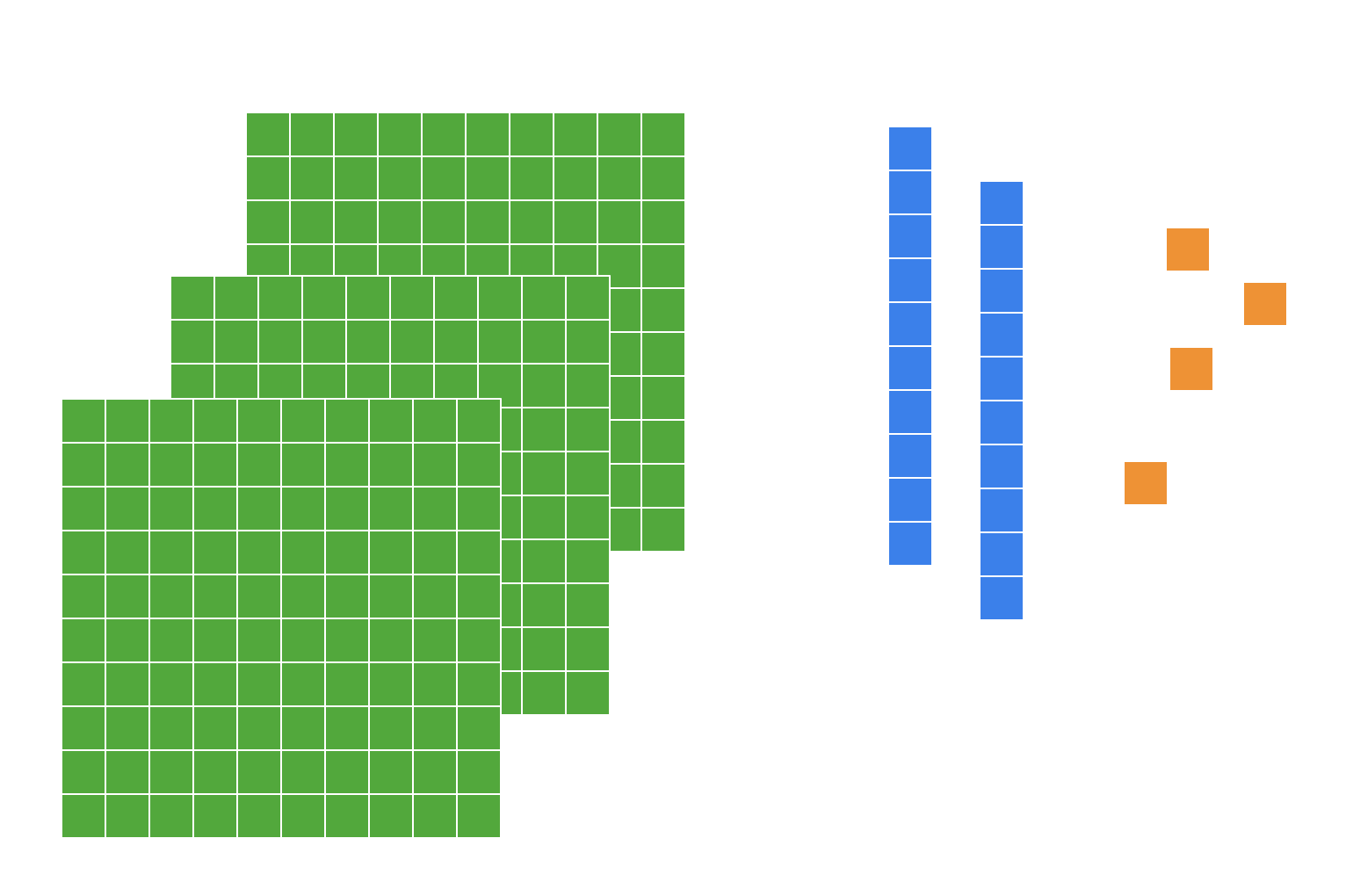
Los números decimales no existen. En todo caso, hablamos de la representación decimal de los números racionales (de ahí las comillas). Y no es sencilla. Y hay que tener en cuenta propiedades de ese conjunto numérico (densidad, especialmente, pero no solo), para que no estemos trabajando con pseudonaturales en lugar de con racionales.
No puedo evitar mencionar el gran trabajo de aula en Primaria de docentes como Manuel Siaba Lestón. En este hilo muestra reflexiones profundas sobre representaciones decimales en un contexto de reparto:
Curso 2022 5º . Recomiendo SISTEMAS DE REPRESENTACIÓN DE NÚMEROS RACIONALES POSITIVOS UN ESTUDIO CON MAESTROS EN FORMACIÓN (Tesis J. M. Gairín Sallán). Y sí ,ahora, el reparto fuera de 5 tortillas 11 personas 🤔

La reflexión más interesante q surge en este momento es q los números q admiten una representación decimal finita también admiten otra infinita, disminuyendo la última cifra significativa y añadiendo una «cola» infinita de nueves.
Grupo de Telegram sobre racionales
Si estás interesado/a en una aproximación con significado a todo lo que tiene que ver con el número racional (medida, magnitudes, fracciones, decimales, proporcionalidad, etc.) este es tu grupo de Telegram: https://t.me/+BBaYf0FZZlszYTc8
Lee el post fijado porque ya hay mucha información y materiales. Internivelar Primaria/ESO.
¡Salu2!