¿Por qué experimentar en probabilidad?

Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.

¿Por qué es necesaria la experimentación (guiada) en el aprendizaje de la probabilidad?, dices mientras lanzas con ingenuidad ese dado de papel. ¿Por qué es necesaria?, ¿y tú me lo preguntas? … Dentro hilo (cuento la secuencia 1º/2º ESO)

Si me seguís, puede que sepáis que habíamos empezado por probabilidad en 1º y 2º ESO. Salvo pequeñas variaciones entre grupos, que ya sabemos que cada uno es un mundo y los profesores tenemos algo de ingenieros (o artistas) en ese sentido, la secuencia es la misma para todos.

El primer día, bueno, la presentación y esa actividad que me he acostumbrado a plantear para ir conociendo a cada clase, su cultura de aula, etc. Básicamente se pregunta: “qué sabes de matemáticas” e “inventa un problema”. Aquí enlace para saber más.

Hubo que tirar mucho de ellos para que pusieran algo de estadística y probabilidad. La geometría no creáis que salía mucho mejor parada… Además, el concepto que tenían de problema no se alejaba mucho del de ejercicio, y siempre eran problemas de situaciones aditivas.

Dedicamos tres semanas a probabilidad. Incluyendo la presentación y un examen de cuaderno, así como actividades de conteo con diagrama de árbol que son también del bloque de números. Estadística han sido dos semanas, pero dedicaremos otro hilo a ello.

¿Os acordáis de la #DidMatCita sobre qué pasa si vamos con un enfoque a través de la resolución de problemas (RP) a una clase con una cultura de aula diferente? Bien, pues el trabajo por parejas o pequeños grupos ya choca.

Lo primero: cada grupo (de 3 o 4) tuvo que construir un dado de papel. Fácil, con el módulo sonobe de origami. Se aprovecha para hablar sobre geometría. En el paso 6, “¿qué figura es esta?”. O, “ahora plegamos por la bisectriz”. Todo esto también da información al profesor.

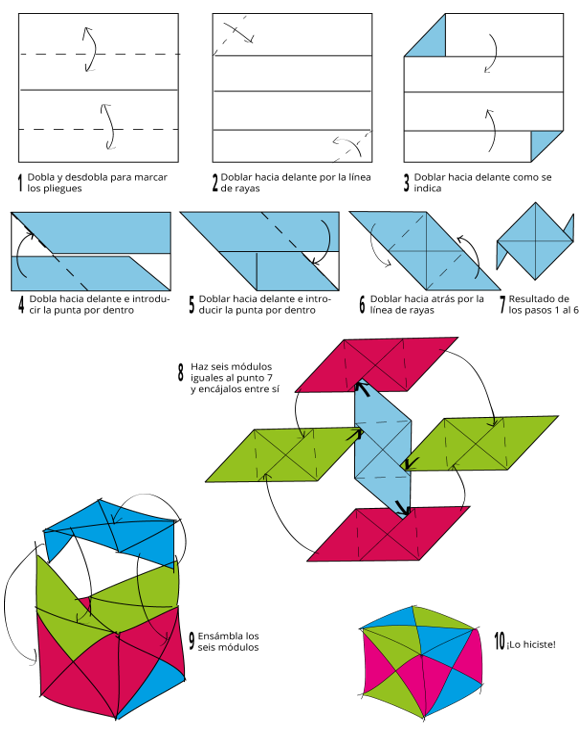
Una vez con el dado, cada grupo lo prueba con el clásico juego de la carrera de coches o caballos. Es decir, apuestan por un número, indicando la razón de su elección (importante esto), y luego juegan. Si hay números no elegidos son PNJ (Personajes No Jugadores) o el “ordenador”.

Las razones de su elección, que a nosotros nos pueden parecer ingenuas, son sus significados personales. Algunos elegían el 3 o el 4 porque no eran números del medio, ni muy altos ni muy bajos. En 1º, muy pocos dijeron que daba igual. En 2º, hubo más.

Ahora, esto es un dado de papel hecho de aquellas maneras (a la foto me remito). A priori, por desconocimiento, la respuesta correcta es la de que da igual. Pero después de jugar, algunos grupos tienen gráficas como estas.

A los de la de colorines. Ahora, ¿qué número creéis que ganará? ¿Da igual? A los de la otra, con estos datos, ¿por cuáles no apostaríais? Con esto entramos no con el significado clásico (regla de Laplace) sino con el frecuencial. Y los vamos a ir conectando.

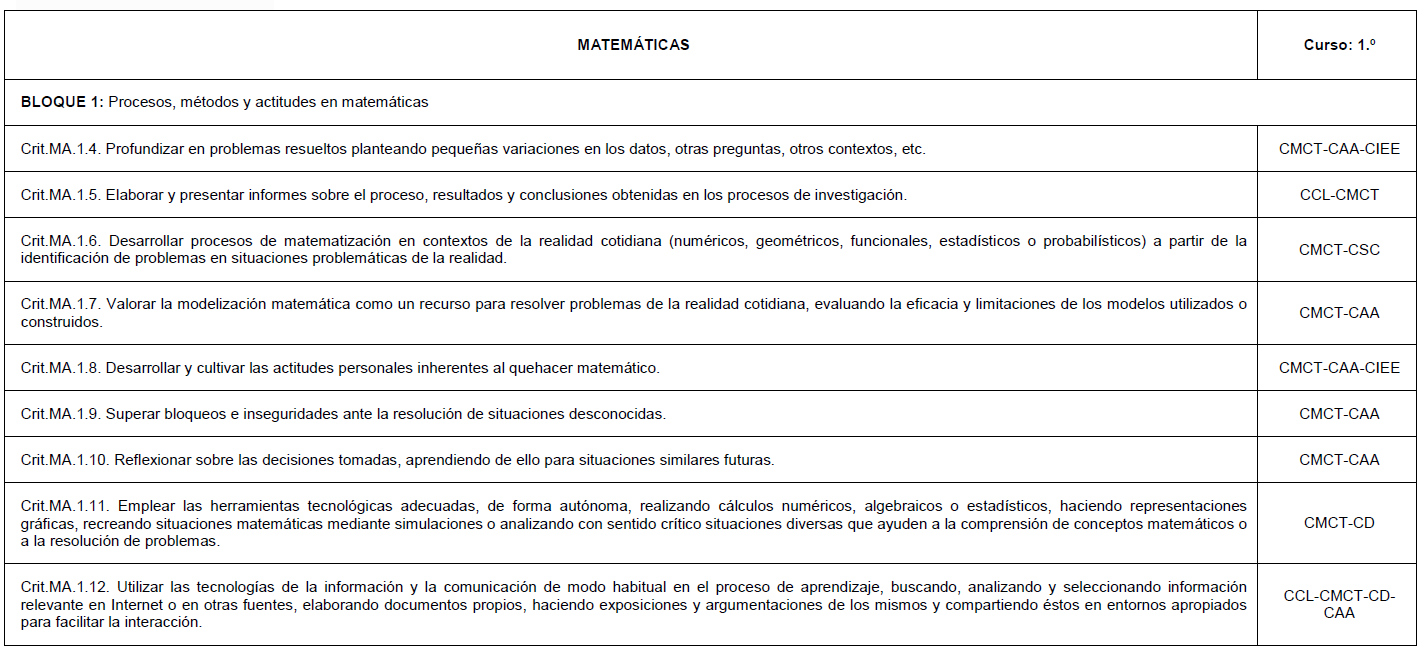
A nivel de contenidos la justificación de realizar esta actividad está clara. Pego aquí lo que tenemos de currículo para el bloque de probabilidad. Desde la didáctica, también, puesto que tratamos de evitar el sesgo de equiprobabilidad, entre otras cosas.

El bloque 1 no lo he pegado porque tendría que haberlo puesto casi entero 😉. Venga, va, que sí, que lo pego. Hay reflexión sobre lo hecho, actitudes personales hacia el quehacer matemático, modelización matemática, investigaciones…

Esta actividad continúa con una pequeña variante. Vamos a trucar el dado para que salga casi siempre “5”. Ahí que los tienes, dándole vueltas al coco. Esto enseguida les sale, poniendo un peso en la cara contraria. Algunos ponen una goma de borrar pegada con celo 😱.

Otros años he planteado actividades similares, incidiendo en lo mismo. Aquí describo una cosilla que hice con la impresora 3D ( enlace aquí)

Se aprovecha para preguntar cómo son los dados comerciales y por qué. Las caras opuestas siempre suman 7. Será por algo, ¿no? Hacemos algún dibujillo de dados irreales en ese sentido.

Después, vamos con el juego que, tal como lo encontré en su día, conozco con el nombre de Beano, aunque hay más variantes. Se dan doce fichas (judías, tapones…) y los jugadores las distribuyen por el tablero.

Se tiran los dados y se suman los resultados. Entonces, cada jugador retira UNA ficha de SU tablero de ese número en cuestión. Si sale el 8, todos retiran una ficha que tengan en el 8. Primero, juegan, sin más. Y sí, el 1 está puesto a propósito.

Hay muchos alumnos, más en 1º que en 2º, pero siempre ocurre, que ponen fichas en el uno. Y aquí es un ejemplo de suceso imposible (luego ponemos nombre a los objetos matemáticos, pero primero dejamos que aparezcan). La primera partida tienden a extenderlos.

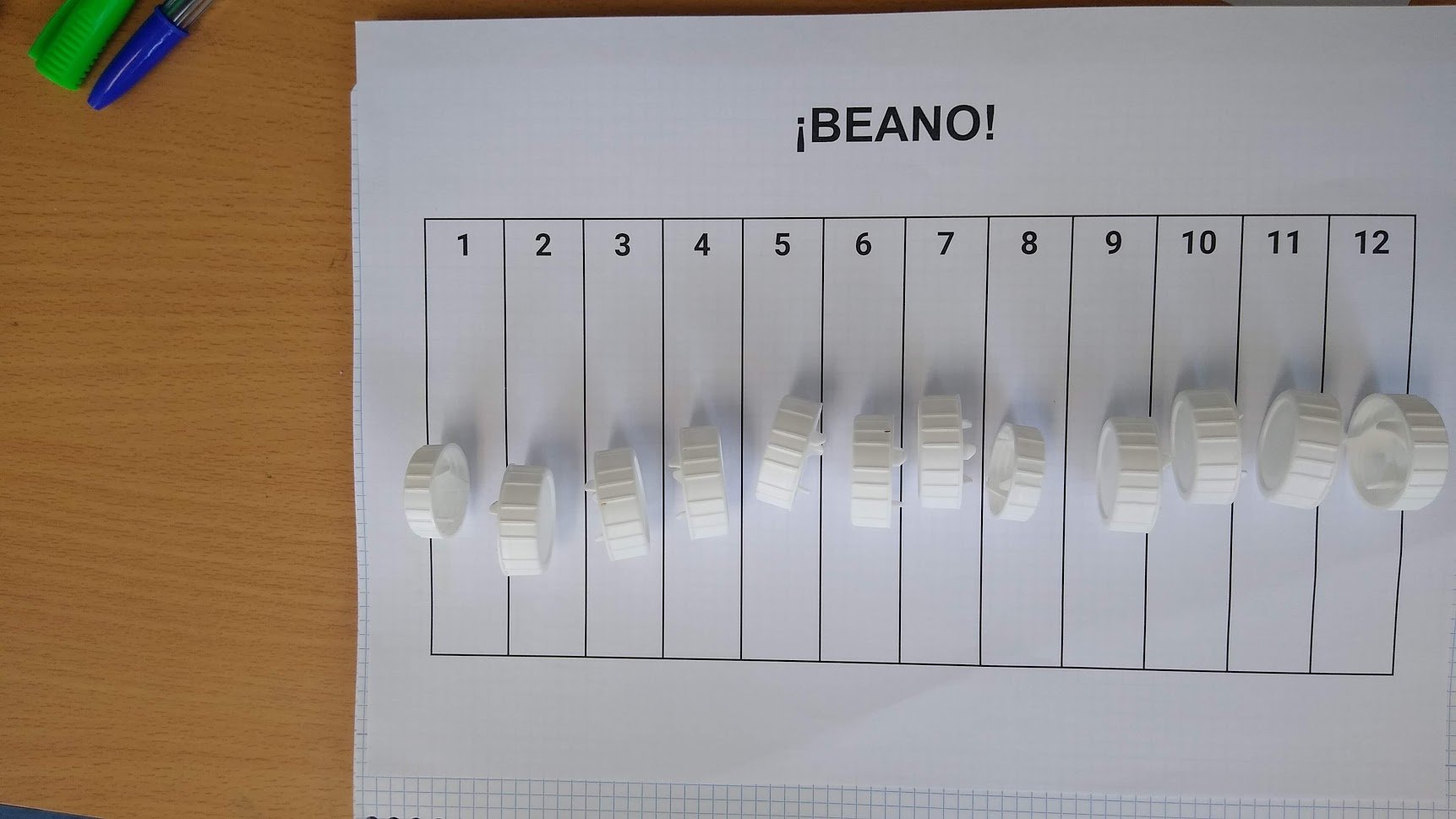
En la segunda, sin tomar datos ni nada, se dan cuenta de que algo pasa. Pero ojo, ¡no es evidente! Es muy común que digan que los números altos salen más. Aunque hay algunos que ya se van oliendo la tostada y perciben que son los del medio. Te encuentras cosas así:

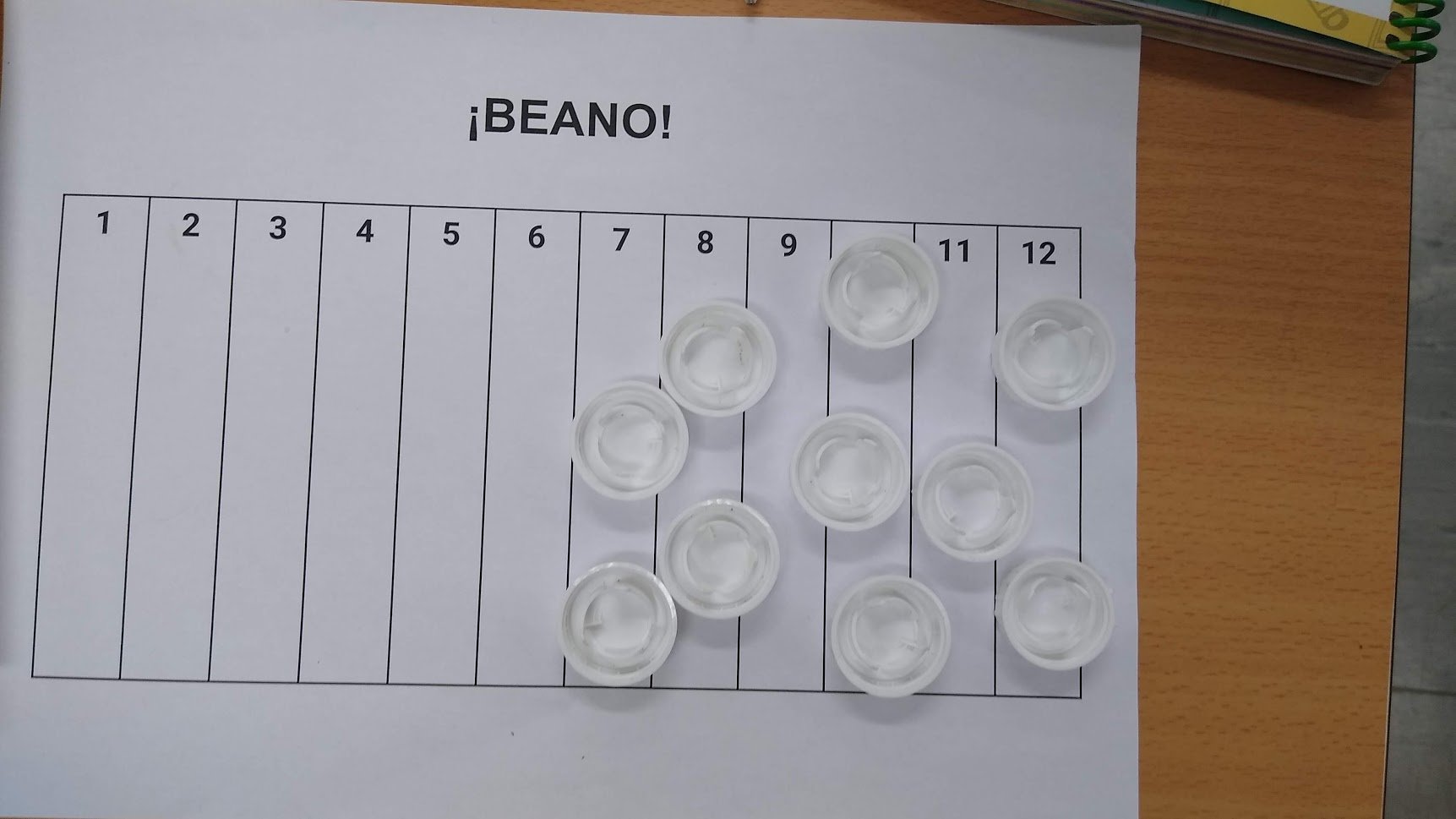
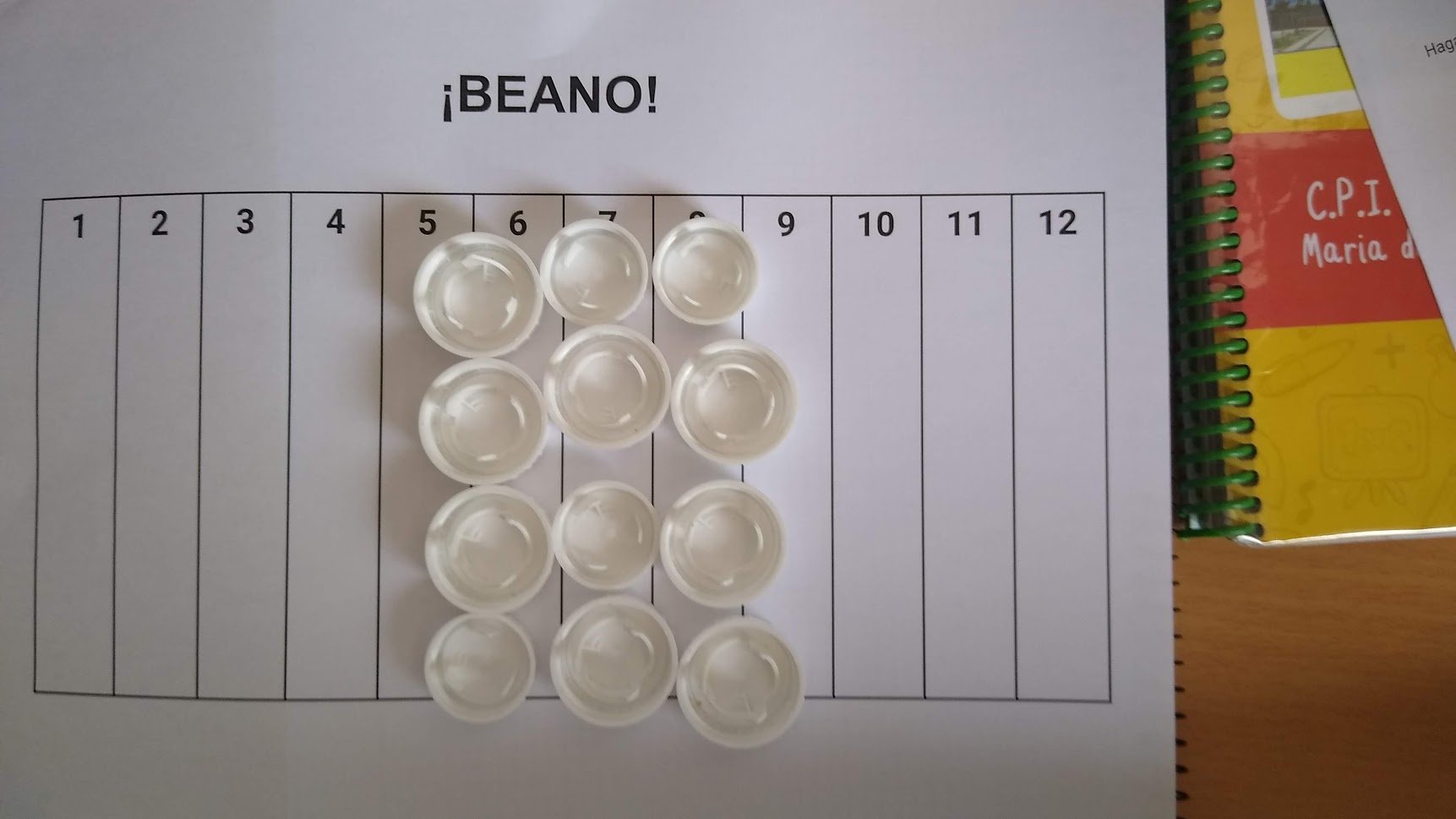
Ahora sí, ahora es cuando se analiza teóricamente lo que está pasando. ¡Hay sumas que salen más! Hay grupos donde cuesta más ver que hay 36 resultados posibles y, además de contarlos en la tabla, hacemos un diagrama de árbol. Si no, los árboles saldrán más adelante.

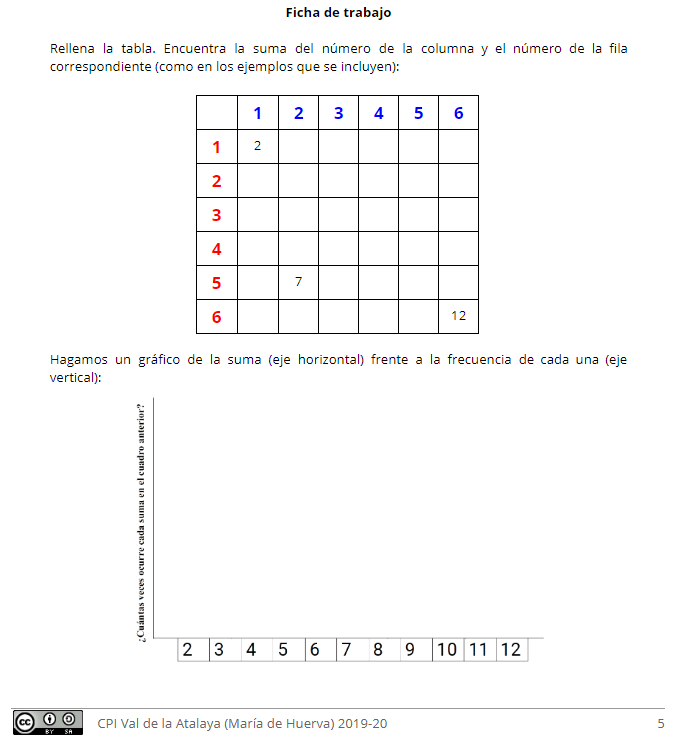
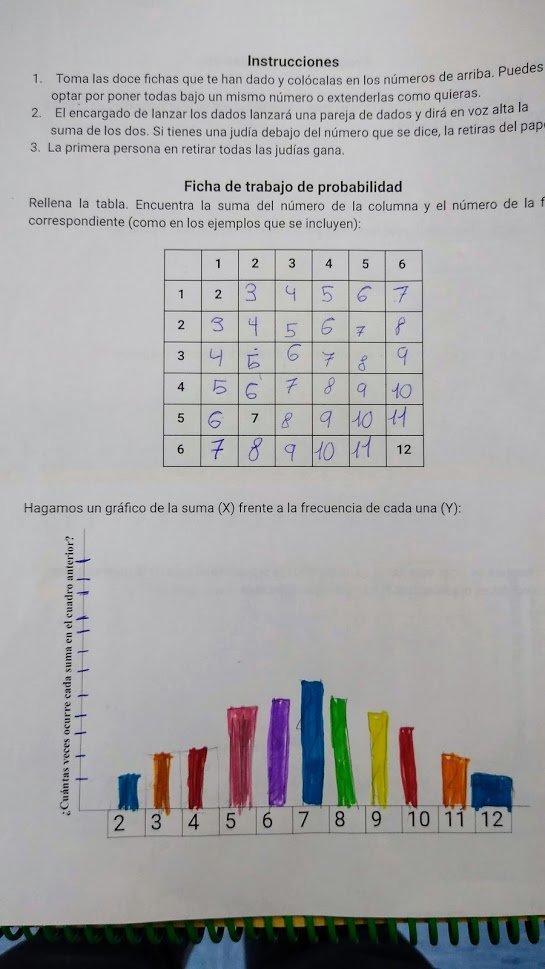
Después de esto puede ser un momento (o en otra actividad posterior) para nombrar y enunciar la regla de Laplace, que salvo lo de Laplace, es algo que han descubierto ellos. En 1º me basta con que me digan que la probabilidad del 7 es 6 de 36.

Quiero decir, que aunque lo introduzco de pasada, no enfatizo apenas la notación P(7)=6/36. Ese P(7), en el fondo, es lenguaje de funciones. Si entramos directamente con la regla de Laplace enunciada así, añadimos una capa de abstracción simbólica innecesaria.

Es importante que quede reflejado el proceso. Por eso, aquí se plantean estas preguntas:

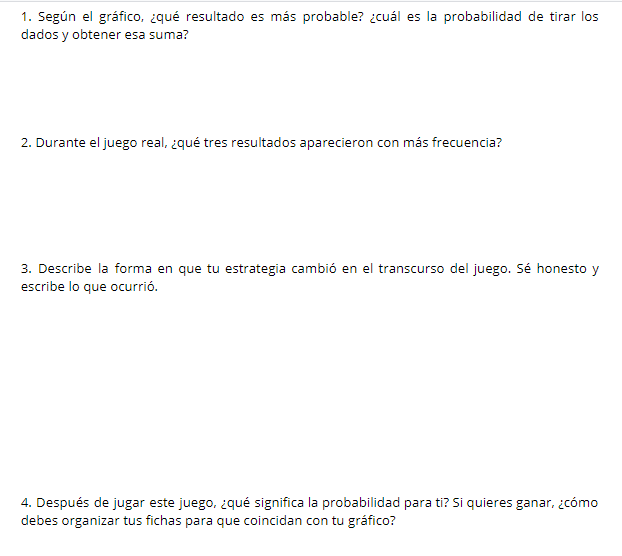
(Nota: el próximo año llamaré al juego TAPONING en lugar de BEANO! y me evitaré la pregunta de por qué se llama así 😊.)

TO BE CONTINUED… Me falta hablar de ruletas, chinchetas, Numb3rs y del tiempo atmosférico. Y del examen de cuaderno que hicimos sobre esto. Pero también me falta tiempo 🤣

Sigamos. Antes de ello, hay quien me ha preguntado si esto vale para primaria. Nada más hacer el hilo, me he auto-retuiteado comentando que muchos de los elementos son válidos para EP. Deseables. Lo del dado de papel lo he hecho como taller en 3º-6º de EP.

En la secuencia hay que meter situaciones donde la regla de Laplace no se pueda aplicar. Por eso ahora viene una actividad con chinchetas. Son dos resultados posibles, o con la punta hacia arriba o tumbadas. La aplicación, sin razonamiento, de Laplace nos diría que es 1/2.

Pues esto lo probamos en clase. Doy a cada grupo un vaso con 10 chinchetas y a probar 10 lanzamientos. Luego, acumulamos el de todos los grupos, con lo que en pocos minutos te juntas con 600 repeticiones. ¡Anda! No se cumple Laplace. Sale un 70-30.

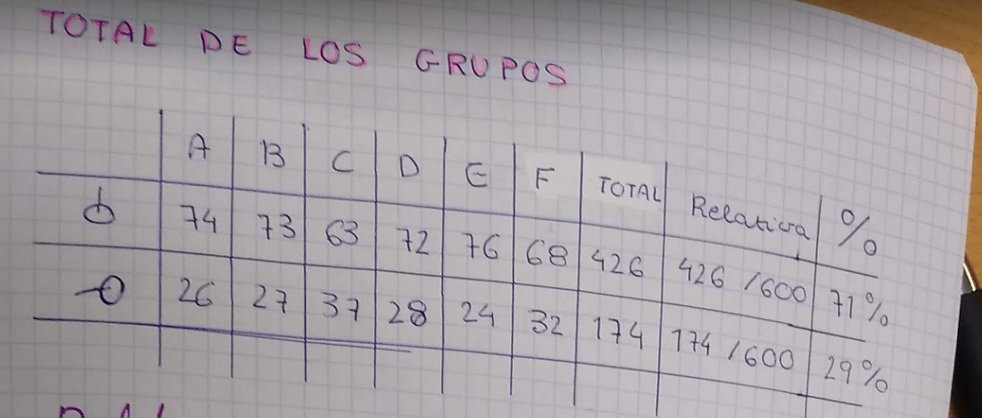
Importante. Antes de empezar tenían que expresar su creencia (subjetiva). Había de todo, desde los que decían que siempre tumbados, hasta los que razonaban que como el culo pesa más, caerían más veces hacia arriba. Otros, con el mismo motivo, decían que no, que tumbadas.

Después, a por las ruletas. En algunas clases no dio tiempo a hacer la experimentación física, que habría sido lo mejor, y fuimos directamente a la experimentación por simulación. Lo mejor, las dos cosas. Ya os decía que había diferencias entre grupos de clase. Pues eso.

Se trata de diseñar una ruleta (se juega con un clip y un boli) de manera que si juegas y eliges primero, tengas mayor probabilidad de ganar que el otro. La imagen de esa ruleta contiene una imprecisión, habla de mayor posibilidad (esto lo veremos después).

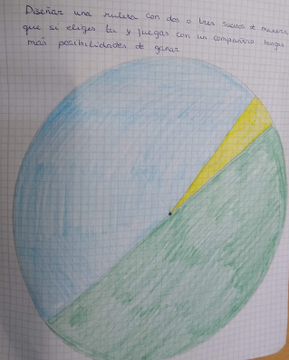
Lo mismo. Dejamos que expresen su intuición y luego contrastamos. Tampoco vamos a hacer un montón de repeticiones, que ya saben de qué va esto. Y haremos una simulación en el ordenador a la vista de todos.

Proponemos el Beano! pero con dos ruletas, como ejercicio. Esto solo lo comento brevemente, incidiendo en que este tipo de cosas se preguntan en el examen de cuaderno. Al día siguiente, alguien pregunta y discutimos sobre ello. También, jugar a mirar la resta en lugar de la suma.

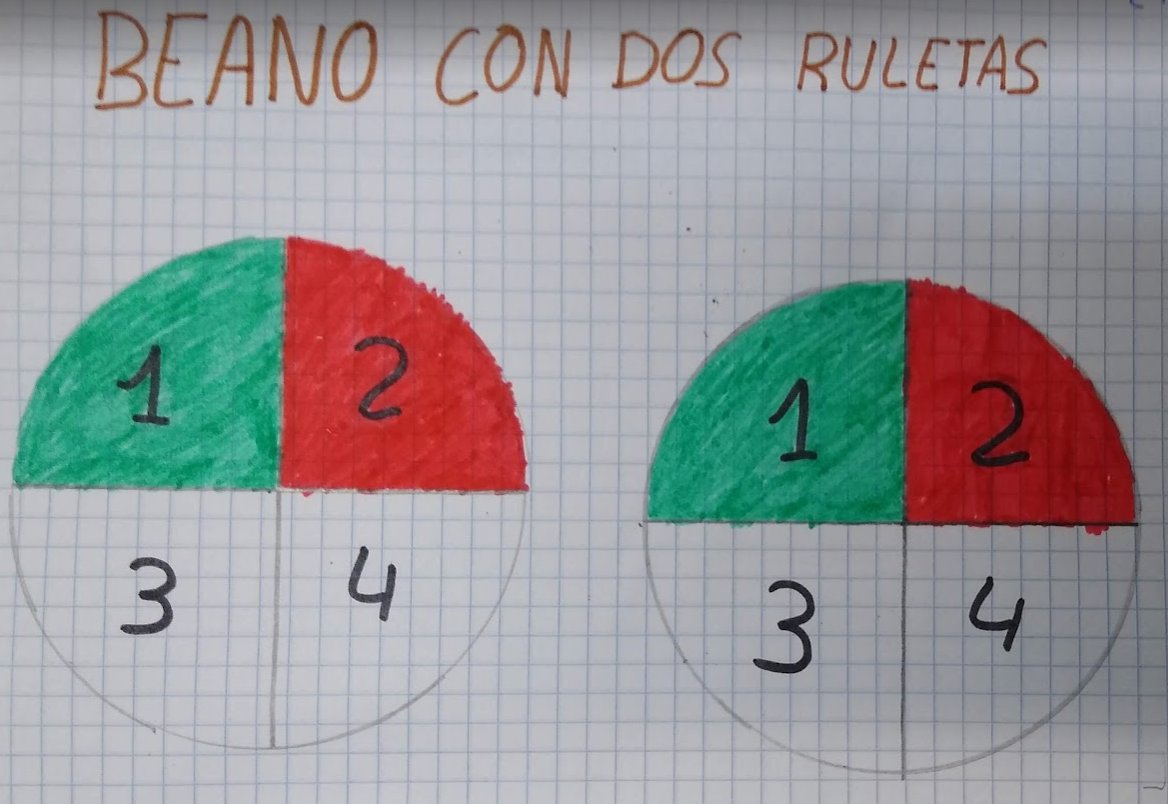
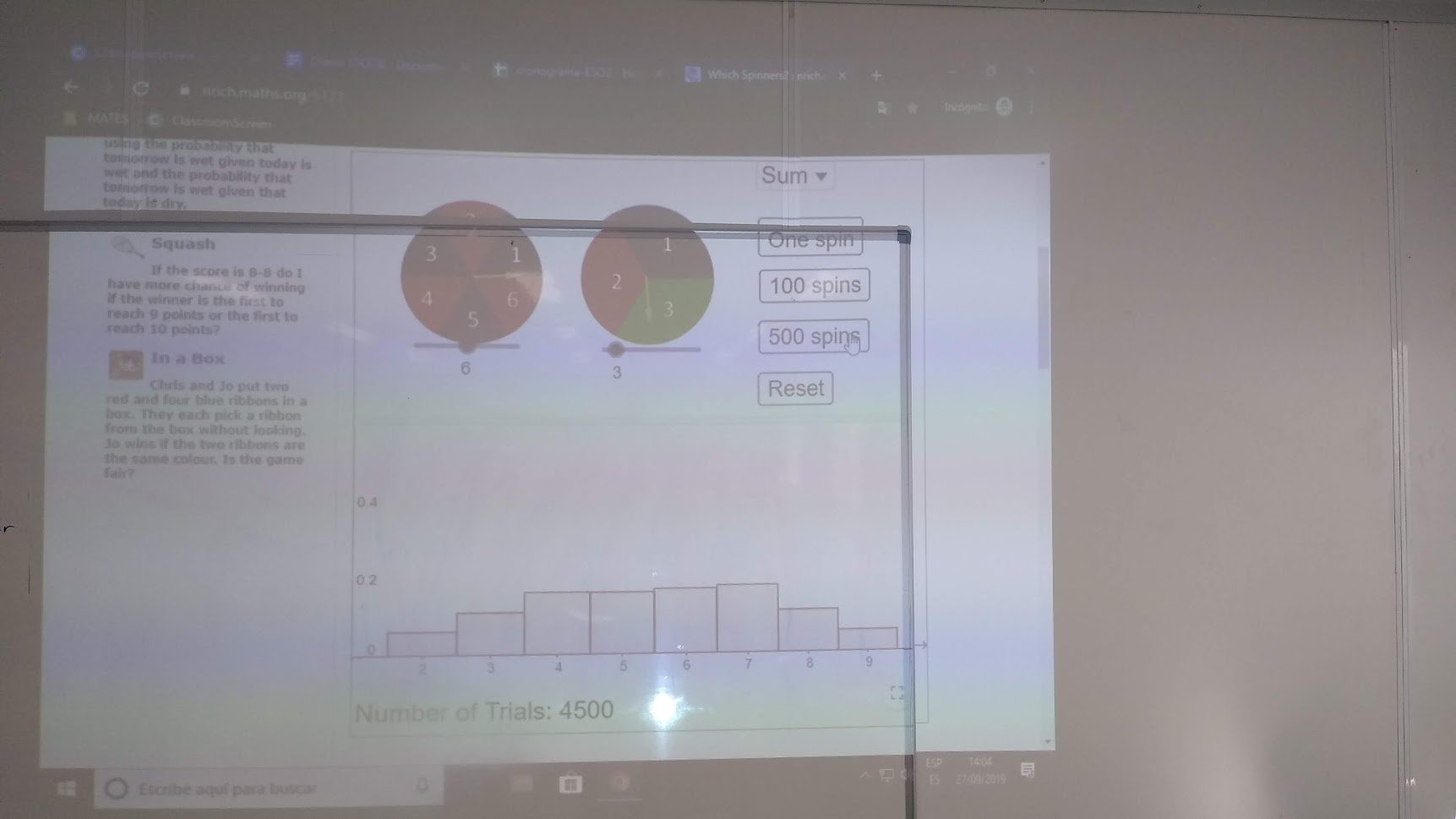
El enlace de las simulaciones de las ruletas es este: https://nrich.maths.org/6123. @nrichmaths es lo más, ¿lo había dicho? El enlace lo tienen a su disposición, además de haberlo probado en clase.

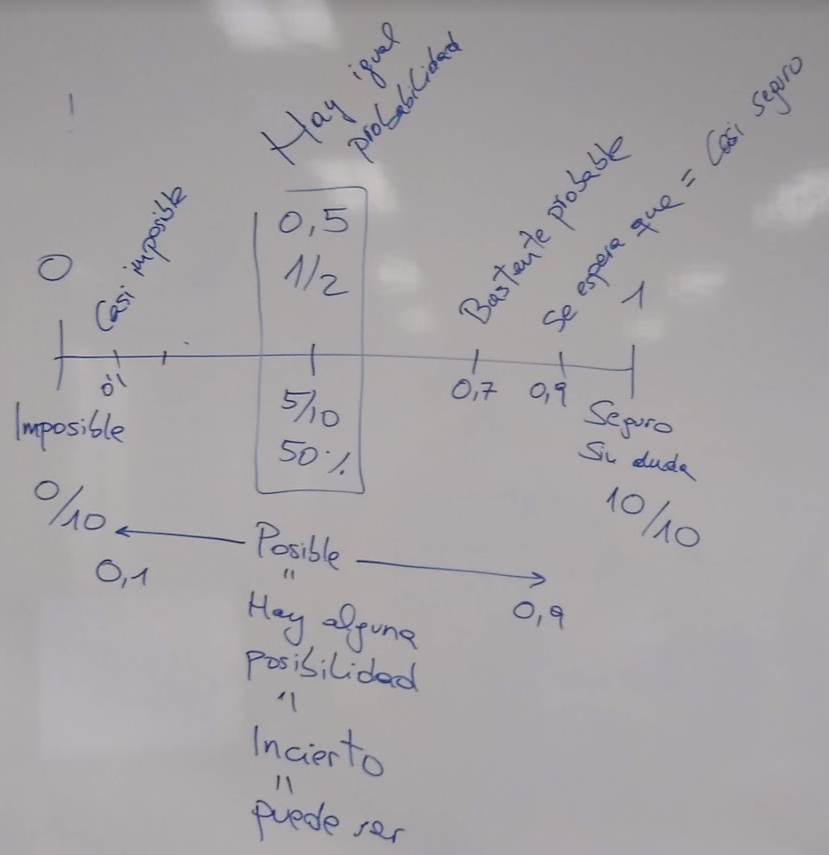
Vamos con una actividad que está sacada, prácticamente tal cual, del librito de @edsintesis de Godino, Batanero y Cañizares. Hay que ordenar palabras, asignarles un número entre 0 y 1 y… bueno, me dicen que esto es Mates, no Lengua. De nuevo, choca con la “cultura de aula”.

Y ahí que estuvimos un rato discutiendo. Primero en pequeño grupo y después en común. Incierto no es imposible, no. Es todo lo que no es cierto. Y no se tiene mayor o menor posibilidad. Nos salió algo así:

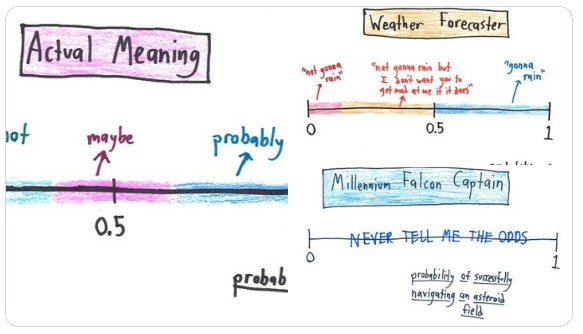
En algunos grupos me puede detener y enseñar esta entrada de @benorlin (soy muy fan, lo sé), donde sale la escala usual de probabilidad, y la probabilidad entendida desde el punto de vista de varias profesiones. Y tal como la entiende Han Solo…

Para completar la cuestión de lenguaje e introducir un tipo de actividad que usaremos mucho, trabajamos este WODB (no dio tiempo en todos grupos, es una pena, sí). Hay que ver cuál es el que no encaja. Y la cosa es que hay que encontrar al menos una razón para cada uno.

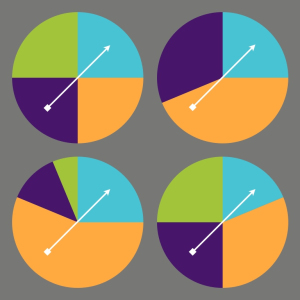
Esto de la WODB lo tenemos publicado en las actas del último simposio de la @_SEIEM @xxiiiseiem2019. Lo presentó maravillosamente Maria Ricart. Aquí enlace al pdf.

Continuamos con la idea de juego justo, que ya habíamos introducido con lo de las ruletas. Aquí sí que vale la regla de Laplace.

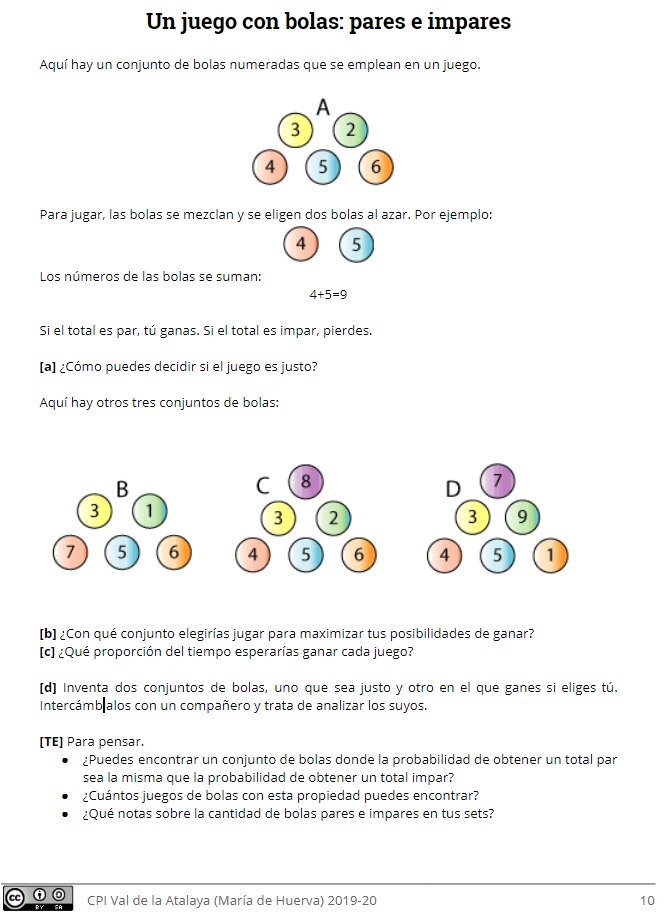
Y terminamos con tareas varias y diagramas de árbol para contar. Esto último ya había aparecido como herramienta en alguna clase donde no quedaba claro el 36 aquel de los posibles resultados al sumar los dos dados.

Y aquí se me acaba el rollo. En 2º se ha hecho lo mismo que en 1º porque el curso pasado no vieron probabilidad tan apenas. Como he dicho, también hay pequeñas variaciones entre clases, que cada una es un mundo.

Este modo de trabajar choca con la cultura de aula. Tienen que pensar, ya habéis visto que a su nivel, y escribir. Y luego razonar. Decía en un tuit que un alumno me pidió, literalmente, hojas de multiplicaciones. Que más de esto no, por favor.

En esas estamos. El trabajo en grupos de 3 o 4 es lo mejor, porque permite irte pasando y controlar de forma más cómoda a todos. Pero hay clases (en este caso una) que me estoy planteando pasar a trabajo por parejas, porque no encuentro solución al tetris.

Y luego está lo del cuaderno. Lo examinamos con examen de cuaderno, donde van tanto preguntas sobre cosas que tienen que estar tal cual, como preguntas que son parecidas a las hechas en clase o las propuestas como ejercicio.

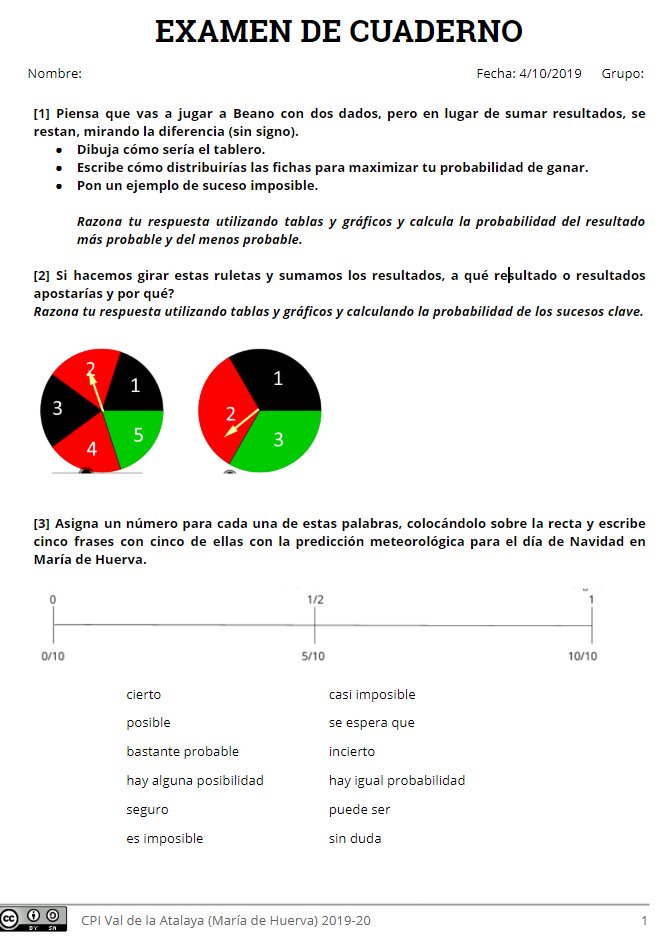
Hubo notas altas y notas bajas. Eso, como siempre, claro. Que a ver si nos vamos a pensar que esta propuesta genera matemáticos en potencia. No. Se trata de dar una respuesta inclusiva para todos y procurar explotar el máximo desarrollo de cada uno.

La cuestión es que entre las notas bajas encontramos alumnos que todavía tienen un desastre de cuaderno (iremos trabajando en ello) como otro perfil que, teniéndolo bonito y completo, está claro que no le sirve como herramienta (también trabajaremos en ello).

Lo del cuaderno es un tema interesante que trataremos otro día. Como aperitivo, os dejo con el enlace de la ponencia del otro día de @Matias_ArceSan en el seminario del @iuma_unizar @dm_unizar en la @FacultadEducaUZ y que hemos subido al canal del grupo: enlace al vídeo

En el turno de preguntas se planteó el dilema. Se piden en 1º y 2º, se corrigen (eventualmente con rúbricas, completitud, organización, …). Luego, en 3º y 4º muchas veces no se piden, creyendo que son autónomos y saben usarlos. ¿Se ha fomentando el trabajo de cuaderno adecuado?

De momento voy a dejarlo aquí, que ya me estoy yendo por las ramas. Feliz clase para todos y enhorabuena si has llegado hasta aquí.

Si te interesan más hilos como este, los voy guardando en mi perfil de Twitter. También intento ponerlos en mi web.

Quiero dar las gracias a mi compañera de no departamento (sic), Ana, porque estar alineados en el mismo enfoque es algo genial. Y sus aportaciones, siempre valiosas.

¡Pero si me había dejado de comentar una de mis actividades favoritas en la secuencia de probabilidad! #AcRiMates La cuento rápido. 👇🏻

Necesito que quitéis todo de la mesa y saquéis 16 objetos. Pueden ser 16 trocitos o gurruños de papel (me olvidé de llevar ese día los tapones del juego de Beano! 🤦🏻‍♂️). ¿Ya los tenéis?

• Ahora vamos a colocarlos de forma aleatoria, al azar, sobre la mesa.

Ahora es cuando vemos el fragmento del primer episodio de la serie Numb3rs. Se hace una breve introducción, contando que son dos hermanos, uno que trabaja en el FBI y que pide ayuda a su hermano, que es matemático. ¡Prohibido tocar los trozos de papel!

Conforme ven el vídeo, ya se van dando cuenta de cómo han colocado ellos los trocitos de papel. La gran mayoría, así:

Claro, son alumnos que los han puesto y los han ido colocando, dejando huecos con una regularidad bastante acusada. ¿Es una configuración posible? Sí, pero muy improbable. Lo más probable es que hubiese amontonamientos, como señala Charlie Eppes.

Esta vez, creo que de 21 alumnos, solo dos hicieron algo así. Que básicamente consiste en dejarlos caer desde cierta altura. O en no toquetearlos demasiado.

Las imágenes son de una clase de 2º ESO. En 1ºESO, más de lo mismo. Pero no creáis que por ser mayorcitos nos salvamos de estos sesgos, que esto lo he hecho con alumnado de máster y también se detecta este fenómeno.

Se enmarca en la distinción de fenómenos aleatorios y deterministas, aunque sobre todo es un primer paso hacia la aceptación de aleatoriedad como modelo matemático. Se distingue entre el proceso de generación (el experimento, colocar los objetos) y el patrón obtenido.

Si alguien quiere profundizar un poquito, Carmen Batanero abordaba estas cosas en las JAEM de 2001.

Como dije en el hilo de la secuencia completa, algunas actividades no pude hacerlas en todos los grupos 😢. Aunque esto es una actividad rica y no lleva mucho tiempo, suma, y debido a ratios o falta de recursos de atención a ACNEAE (apoyos en el aula, …) no pude encajarla.