Atención a la diversidad a través de la resolución de problemas
Lo que viene a continuación es una versión blog o desplegada de este hilo de Twitter.
Un aspecto que me fascina de la enseñanza a través de la resolución de problemas es cómo permite la inclusión y la atención a la diversidad. Os cuento algo al respecto.
Si queremos atender a la diversidad, la opción, por sistema, de dar unas fichas para los que van más rezagados y material extra para los que tienen mayor capacidad, no hace sino excluir dentro del aula.
La inclusión y la igualdad de oportunidades tiene lugar cuando la tarea de clase es la misma para todos. Lo que se consigue con actividades del tipo “suelo bajo y techo alto” (low floor high ceiling).
El otro día puse el ejemplo de la actividad de la mediatriz, o del punto de encuentro. Empieza con tareas muy sencillas que puede abordar todo el mundo. Colocar un punto, medir distancias, observar…
De hecho, esa parte, que podría plantearse en primaria, no sobra para nadie. Porque contribuye a desarrollar el significado de mediatriz como lugar geométrico.
Conforme avanza la secuencia de actividades, hay puntos, como el que voy a comentar, que denotan que el aprendizaje no es el mismo para todos (no puede ser de otra manera).
En una de las actividades, se trata de averiguar el circuncentro de algunos cuadriláteros: cuadrado, rectángulo, trapecio isósceles, trapecio rectángulo.
El del trapecio rectángulo no se puede hacer, claro, si trazas las mediatrices no se cortan en el mismo punto. Aquí es donde una alumna de 1º ESO ha realizado la siguiente observación. Interesante es poco.
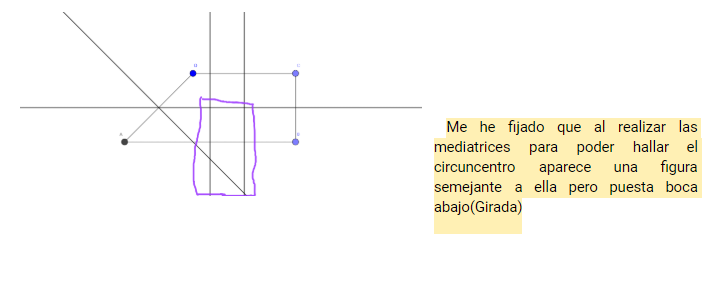
En clase presencial puedes animar a los alumnos a realizar este tipo de observaciones, eligiendo bien las preguntas. Sin embargo, la interacción online es muchísimo más reducida. Por eso me alegro tanto cuando veo estos indicios.
Le pregunté que cómo podía estar segura de lo que decía, y que se animara a utilizar las herramientas de medida de geogebra.
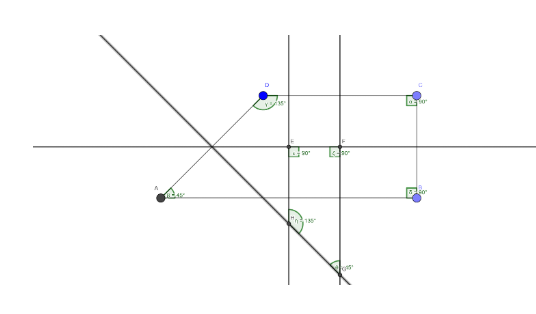
Después, le propuse pensar acerca del porqué de que ocurra, que implica propiedades de la mediatriz y de ángulos, así como aspectos de perpendicularidad y semejanza.
En fin, que solo venía a compartir esta pequeña alegría en tiempos de crisis. Porque las matemáticas serán maravillosas, pero también pueden ser muy segregadoras, separando entre los que controlan y los que no.
Un aprendizaje inclusivo no implica que todos terminen aprendiendo lo mismo. Se trata de equidad y de permitir y buscar el máximo desarrollo de cada uno.